65 Is What Percent Of 80
sandbardeewhy
Nov 27, 2025 · 9 min read
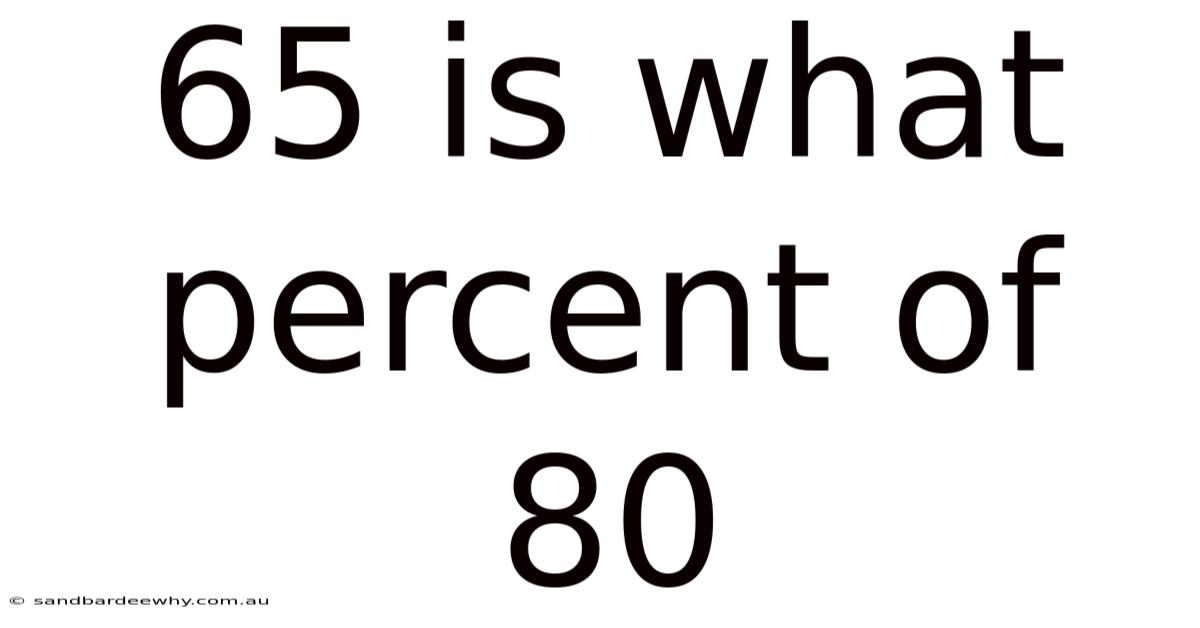
Table of Contents
Imagine you're at a bustling farmer's market, eyeing a beautiful basket of ripe, red apples. The sign says "80 Apples, Special Today!" But as you start counting, you realize there are only 65 apples in the basket. A little perplexed, you wonder, "What portion of the advertised total am I actually getting?" This simple question mirrors the everyday math problem: 65 is what percent of 80?
This isn't just about apples; it's about understanding proportions, a fundamental concept that threads through many aspects of life. From calculating discounts at your favorite store to figuring out how much of your monthly budget goes towards rent, understanding percentages and how to calculate them is a crucial skill. So, how do we solve this common question? Let's dive in and explore the answer and practical uses of understanding percentage calculations.
Main Subheading
Percentages are a fundamental tool in mathematics, frequently used to express proportions and ratios. They provide a standardized way to understand parts of a whole, making comparisons straightforward and intuitive. The concept of percentages isn't just confined to classrooms; it permeates daily life, influencing financial decisions, statistical analyses, and even simple tasks like calculating tips at a restaurant.
Understanding percentages involves grasping how they relate to fractions and decimals, and how to convert between these forms. This knowledge empowers individuals to interpret data accurately, make informed decisions, and solve practical problems efficiently. Whether you're calculating discounts, analyzing sales figures, or understanding survey results, a solid grasp of percentages is indispensable.
Comprehensive Overview
At its core, a percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." This etymology highlights the basic idea: a percentage tells you how many parts out of 100 you have.
Mathematically, a percentage is calculated by dividing the part by the whole and then multiplying by 100. The formula is:
Percentage = (Part / Whole) * 100
For example, if you have 30 apples out of a total of 100, then you have 30%. If you have 50 apples out of 200, the calculation would be (50 / 200) * 100 = 25%. This illustrates how percentages standardize comparisons, making it easy to understand proportions relative to a common base.
Percentages are closely related to both fractions and decimals. A percentage can be easily converted into a fraction by placing it over 100 and simplifying. For instance, 25% is equivalent to 25/100, which simplifies to 1/4. This fraction represents the same proportion as the percentage.
Similarly, a percentage can be converted into a decimal by dividing it by 100. For example, 75% becomes 0.75 when divided by 100. Decimals provide another way to represent proportions, and the ability to convert between percentages and decimals is crucial for many calculations.
The history of percentages dates back to ancient Rome, where calculations involving hundredths were used for taxation and trade. However, the modern concept of percentages became more formalized during the Renaissance, as trade and commerce expanded. The use of the percent sign (%) evolved over time from various abbreviations used in medieval manuscripts.
Today, percentages are used in almost every field. In finance, they are essential for calculating interest rates, investment returns, and inflation rates. In statistics, percentages are used to present data in a clear and understandable format. In retail, discounts and sales taxes are expressed as percentages. Their versatility and ease of understanding make percentages an indispensable tool in numerous contexts. Understanding how to calculate and interpret percentages is therefore a vital skill for anyone navigating the modern world.
Trends and Latest Developments
The application of percentages continues to evolve with new trends and technological advancements. One significant trend is the increasing use of data analytics, where percentages play a crucial role in interpreting large datasets. Businesses use percentages to analyze sales trends, customer behavior, and market performance. For instance, retailers track the percentage increase in sales during promotional periods to gauge the success of their marketing campaigns.
Another notable trend is the use of percentages in health and fitness tracking. Wearable devices and apps provide users with data on their daily activity levels, expressed as percentages of their goals. This allows individuals to monitor their progress and make informed decisions about their health and fitness routines.
Moreover, there is growing awareness of the importance of understanding percentages in financial literacy. Many educational programs now emphasize the need for individuals to grasp concepts like compound interest, inflation, and investment returns, all of which rely heavily on percentages. This increased focus aims to empower individuals to make sound financial decisions and avoid common pitfalls.
The latest developments also include the use of percentages in artificial intelligence and machine learning. Algorithms use percentages to assess the accuracy of predictions and the reliability of models. For example, in medical diagnostics, AI systems might report the probability of a particular diagnosis as a percentage, helping doctors make more informed decisions.
Professional insights highlight the critical role of percentages in effective communication. Whether presenting financial reports, marketing strategies, or scientific findings, the ability to use percentages to convey information clearly and concisely is highly valued. Professionals across various fields emphasize the need to avoid misleading or ambiguous use of percentages, ensuring that data is presented accurately and ethically.
Tips and Expert Advice
Calculating percentages can be straightforward with the right approach. Here are some practical tips and expert advice to help you master percentage calculations:
-
Understand the Basics: Before diving into complex problems, ensure you understand the fundamental formula:
Percentage = (Part / Whole) * 100. Knowing this formula is the foundation for all percentage calculations. -
Identify the Part and the Whole: Accurately identifying the part and the whole is crucial. The "part" is the value you are comparing, and the "whole" is the total or base value. For example, if you want to find what percentage 30 is of 50, 30 is the part and 50 is the whole. Misidentifying these values will lead to incorrect results.
-
Convert Percentages to Decimals: When performing calculations involving percentages, converting percentages to decimals can simplify the process. To convert a percentage to a decimal, divide it by 100. For instance, 25% becomes 0.25. Multiplying by the decimal equivalent can often be easier than working with percentages directly.
-
Use Proportions: Setting up proportions is a powerful technique for solving percentage problems. A proportion is an equation stating that two ratios are equal. For example, if you know that x% of 80 is 20, you can set up the proportion:
x/100 = 20/80. Solving for x will give you the percentage. -
Estimate and Check Your Answers: Always estimate your answer before performing the calculation to ensure your final result is reasonable. For example, if you are calculating what percentage 48 is of 100, you know the answer should be close to 50%. After calculating, check your answer to ensure it makes sense in the context of the problem.
-
Practice Regularly: Like any skill, mastering percentage calculations requires practice. Work through a variety of problems, from simple to complex, to build your confidence and proficiency. Online resources, textbooks, and practice worksheets can be valuable tools for improving your skills.
-
Use Technology Wisely: Calculators and spreadsheet software like Excel can be helpful for performing percentage calculations quickly and accurately. However, it's important to understand the underlying concepts and not rely solely on technology. Use technology as a tool to enhance your understanding, not replace it.
-
Apply Percentages to Real-Life Scenarios: To reinforce your understanding, apply percentages to real-life scenarios. Calculate discounts when shopping, figure out tips at restaurants, or analyze your personal budget using percentages. Applying percentages to practical situations will make the concept more relevant and easier to remember.
By following these tips and expert advice, you can improve your understanding of percentages and confidently tackle a wide range of percentage-related problems.
FAQ
Q: How do I calculate the percentage increase or decrease?
A: To calculate the percentage increase or decrease, use the formula: [(New Value - Old Value) / Old Value] * 100. If the result is positive, it's a percentage increase. If it's negative, it's a percentage decrease.
Q: What is the difference between percentage and percentage points?
A: A percentage is a proportion out of 100, while percentage points refer to the arithmetic difference between two percentages. For example, if a value increases from 10% to 12%, the increase is 2 percentage points.
Q: How do I find the original value if I know the percentage and the result?
A: To find the original value, divide the result by the percentage (expressed as a decimal). For example, if 20% of a number is 50, the original number is 50 / 0.20 = 250.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when comparing a new value to an original value where the new value is more than double the original. For example, if a company's revenue doubles, the percentage increase is 100%, and if it more than doubles, the percentage increase will be greater than 100%.
Q: How do I calculate a percentage of a percentage?
A: To calculate a percentage of a percentage, convert both percentages to decimals and multiply them. For example, to find 10% of 50%, convert them to 0.10 and 0.50, then multiply: 0.10 * 0.50 = 0.05, which is 5%.
Conclusion
So, to answer the initial question, 65 is what percent of 80? The calculation is (65 / 80) * 100 = 81.25%. Therefore, 65 is 81.25% of 80. Understanding percentages is more than just solving math problems; it's about gaining a powerful tool for interpreting the world around you. From calculating discounts to analyzing financial data, percentages provide a clear and standardized way to express proportions and make informed decisions.
We encourage you to put these concepts into practice. Whether you're managing your budget, evaluating investment opportunities, or simply trying to understand the latest news, a solid understanding of percentages will serve you well. Share this article with friends and family to help them improve their understanding of percentages and empower them to make better decisions in their daily lives.
Latest Posts
Latest Posts
-
How Many Ounces In A 5 Gallon
Nov 27, 2025
-
What Percent Of 300 Is 50
Nov 27, 2025
-
For Each Relation Decide If It Is A Function
Nov 27, 2025
-
How Does Friction Affect The Motion Of Objects
Nov 27, 2025
-
Stages Of Healing 3rd Degree Burn
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about 65 Is What Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.