9 Is What Percent Of 20
sandbardeewhy
Nov 24, 2025 · 9 min read
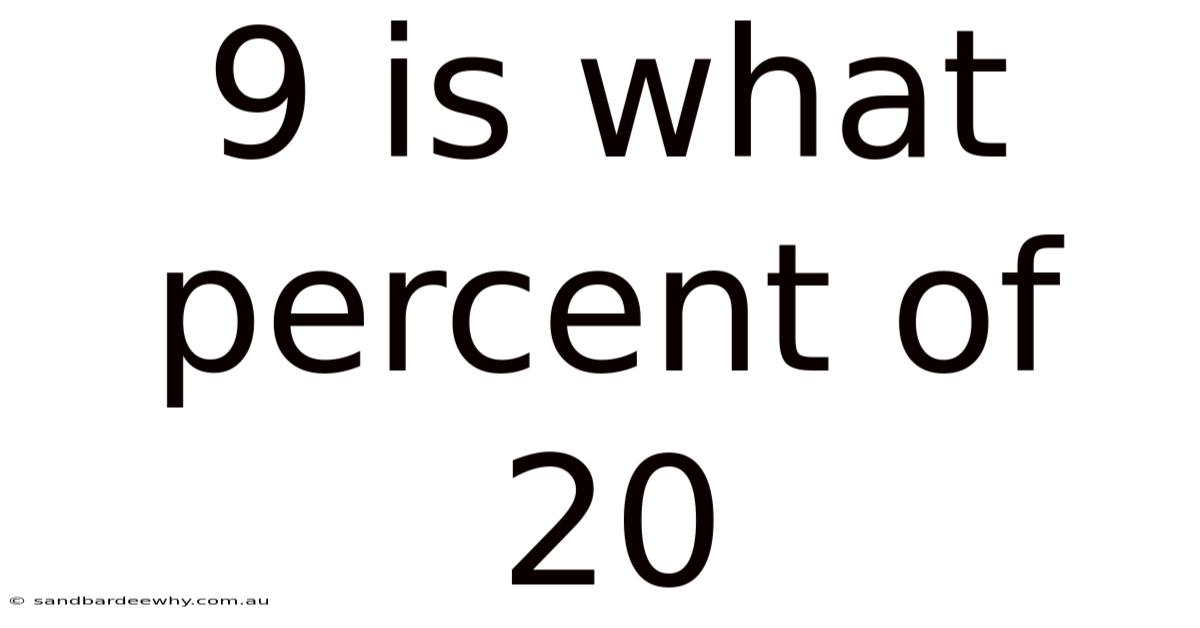
Table of Contents
Imagine you're at a bustling farmers market, eyeing a basket of plump, juicy apples. The vendor tells you that 20 of these apples are on special, but only 9 are the variety you absolutely love. Suddenly, a question pops into your head: "What percentage of these apples are my favorite kind?" This simple scenario introduces a common type of problem that many face daily – calculating percentages.
Percentage calculations are more than just a math exercise; they are a fundamental tool for understanding proportions, making comparisons, and interpreting data in various contexts. Whether it's determining discounts at a store, understanding statistical data, or figuring out proportions in a recipe, knowing how to calculate percentages is an essential skill. In this article, we will delve into solving the question "9 is what percent of 20?" and explore the broader applications of percentage calculations in everyday life.
Main Subheading
Understanding percentages involves grasping the relationship between a part and a whole. At its core, a percentage represents a fraction of 100, indicating how much of something is present relative to the entire amount. The concept is deeply rooted in the idea of proportionality, allowing us to express proportions in a standardized and easily understandable format. The question "9 is what percent of 20?" is a classic example of this relationship, requiring us to determine what fraction of 20 is represented by 9, and then express that fraction as a percentage.
The significance of understanding percentages extends beyond mere mathematical curiosity; it permeates numerous facets of daily life and professional fields. In finance, percentages are used to calculate interest rates, investment returns, and profit margins. In retail, they help consumers understand discounts, sales tax, and markups. In science and statistics, percentages are used to analyze data, present research findings, and compare different groups. Understanding how to calculate and interpret percentages empowers individuals to make informed decisions, analyze data effectively, and communicate quantitative information clearly.
Comprehensive Overview
The concept of percentage traces its origins back to ancient Rome, where the Romans dealt with fractions based on one hundred, known as centesima. As trade and commerce flourished, the need for a standardized way to calculate taxes, interest, and proportions became increasingly important. Although the modern symbol for percent (%) did not exist at the time, the idea of dividing quantities into hundredths was well-established.
During the Middle Ages, with the spread of Arabic numerals and mathematical knowledge, the use of percentages became more formalized. The term "percent" comes from the Latin per centum, meaning "out of one hundred." By the 15th century, merchants, bankers, and mathematicians frequently used percentage calculations in their daily transactions. The adoption of the percent symbol (%) is attributed to the evolution of abbreviations for per cento over time. Today, the concept of percentage is universally recognized and applied across various fields, making it an indispensable tool for quantitative analysis and communication.
To calculate what percentage one number is of another, you can use a straightforward formula:
Percentage = (Part / Whole) * 100
In the question "9 is what percent of 20?", 9 represents the part, and 20 represents the whole. By applying the formula, we can easily find the percentage.
Percentage = (9 / 20) * 100
First, divide 9 by 20:
9 / 20 = 0.45
Next, multiply the result by 100:
0.45 * 100 = 45
Therefore, 9 is 45% of 20. This calculation provides a clear and concise way to express the proportion of 9 relative to 20, highlighting the usefulness of percentages in simplifying comparative data.
Percentages are used in various real-world scenarios. Consider a retail setting where a store offers a 25% discount on a $100 item. To calculate the discount amount, you multiply the original price by the percentage:
Discount Amount = $100 * (25 / 100) = $25
The final price after the discount is:
Final Price = $100 - $25 = $75
Another example is calculating a grade on a test. If a student scores 80 out of 100, their percentage score is:
Percentage Score = (80 / 100) * 100 = 80%
These examples demonstrate how percentages are used to simplify and standardize comparisons, making them an essential tool in various practical applications.
To deepen your understanding, let’s consider some additional examples. Suppose you want to find out what percentage 30 is of 50. Using the formula:
Percentage = (30 / 50) * 100
Percentage = 0.6 * 100
Percentage = 60%
This means 30 is 60% of 50.
In another scenario, let's say you want to determine what percentage 15 is of 75:
Percentage = (15 / 75) * 100
Percentage = 0.2 * 100
Percentage = 20%
Therefore, 15 is 20% of 75. These examples illustrate the versatility of percentages in representing proportions and making comparisons across different numerical scales.
Trends and Latest Developments
Current trends indicate an increasing reliance on data analysis and interpretation in various sectors, making percentage calculations more relevant than ever. From financial markets to healthcare, the ability to understand and communicate proportions effectively is crucial for decision-making. In finance, for example, investors use percentage changes to assess the performance of stocks, bonds, and other assets. Recent data shows that a growing number of individuals are using online tools and apps to calculate investment returns and manage their portfolios.
In the retail sector, businesses use percentages to analyze sales trends, determine pricing strategies, and evaluate the effectiveness of marketing campaigns. According to recent market research, retailers are increasingly leveraging data analytics to personalize promotions and offer targeted discounts to customers. Furthermore, percentages play a vital role in scientific research, where they are used to analyze experimental data, compare different groups, and draw conclusions. For example, in medical studies, researchers use percentages to report the effectiveness of treatments and the prevalence of diseases.
The rise of data visualization tools has also contributed to the increased use of percentages in communication. Charts and graphs often use percentages to present data in a clear and concise manner, making it easier for audiences to understand complex information. Professional insights highlight the importance of data literacy in today's world, emphasizing the need for individuals to develop strong analytical skills to interpret and communicate data effectively.
Tips and Expert Advice
When working with percentages, avoid common mistakes by understanding the context and applying the correct formulas. One frequent error is confusing the part and the whole in the calculation. Always ensure that the part represents the specific portion you are interested in, and the whole represents the total amount or reference value. For example, if you are calculating the percentage increase in sales, the increase amount is the part, and the original sales figure is the whole.
Another common mistake is misinterpreting the results. A percentage represents a proportion relative to 100, so understanding what the base value represents is crucial. For instance, a 10% increase on a small number might be negligible in absolute terms, whereas a 10% increase on a large number could be substantial. Being mindful of the underlying values helps to provide a more accurate interpretation of the percentage.
To improve your accuracy in percentage calculations, use estimation techniques to check your answers. Before performing the calculation, try to approximate the percentage in your head. For example, if you are calculating what percentage 48 is of 100, you can quickly estimate that it is close to 50%. This mental check can help you identify obvious errors in your calculations.
Another useful technique is to convert percentages into decimals or fractions before performing calculations. For instance, 25% is equivalent to 0.25 as a decimal and 1/4 as a fraction. Converting percentages into these forms can simplify calculations and reduce the likelihood of errors. Additionally, it is beneficial to practice percentage calculations regularly to build confidence and proficiency. The more you work with percentages, the more comfortable and accurate you will become.
For advanced percentage calculations, consider using spreadsheet software like Microsoft Excel or Google Sheets. These tools offer built-in functions and formulas for performing complex percentage calculations, such as calculating compound interest or analyzing statistical data. Using spreadsheet software can also help you organize and visualize your data, making it easier to identify patterns and trends.
Furthermore, it is essential to stay updated on the latest trends and best practices in data analysis and interpretation. Following reputable sources of information, such as financial news outlets, academic journals, and industry publications, can help you stay informed about the latest developments in the field. Continuously expanding your knowledge and skills will enable you to use percentages more effectively in various professional and personal contexts.
FAQ
Q: What is a percentage? A: A percentage is a way of expressing a number as a fraction of 100. It is often denoted by the percent sign (%).
Q: How do I calculate what percentage one number is of another? A: Use the formula: Percentage = (Part / Whole) * 100.
Q: Can a percentage be greater than 100%? A: Yes, if the part is greater than the whole. For example, if you have a 200% increase, it means the new value is twice the original value.
Q: How do I convert a percentage to a decimal? A: Divide the percentage by 100. For example, 25% is equal to 0.25.
Q: How do I convert a decimal to a percentage? A: Multiply the decimal by 100. For example, 0.75 is equal to 75%.
Q: What are some common uses of percentages in everyday life? A: Percentages are used in finance (interest rates), retail (discounts), statistics (data analysis), and many other areas to express proportions and make comparisons.
Q: How can I improve my percentage calculation skills? A: Practice regularly, use estimation techniques to check your answers, and leverage tools like spreadsheet software for complex calculations.
Conclusion
In summary, understanding how to calculate percentages is an essential skill with broad applications in everyday life and professional fields. By mastering the formula Percentage = (Part / Whole) * 100, you can accurately determine proportions, make informed decisions, and interpret data effectively. The question "9 is what percent of 20?" is a fundamental example of this calculation, illustrating how percentages can simplify comparisons and provide valuable insights.
From calculating discounts at a store to analyzing financial data, percentages are a powerful tool for understanding the relationship between different quantities. By avoiding common mistakes, using estimation techniques, and leveraging available resources, you can improve your accuracy and confidence in percentage calculations. Now that you understand how to calculate percentages, take the next step and apply this knowledge to real-world scenarios. Practice with different examples, explore advanced techniques, and continue to expand your understanding of this essential concept. Engage with others by sharing your insights and experiences, and encourage them to explore the power of percentage calculations in their own lives.
Latest Posts
Latest Posts
-
How Many Groups Of 5 6 Are In 1
Nov 24, 2025
-
How To Say Be Safe In Spanish
Nov 24, 2025
-
How Does Meiosis Contribute To Genetic Variation In Offspring
Nov 24, 2025
-
9 Is What Percent Of 20
Nov 24, 2025
-
Practice Test For Licensed Practical Nurse
Nov 24, 2025
Related Post
Thank you for visiting our website which covers about 9 Is What Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.