Percentage Of 7 Out Of 12
sandbardeewhy
Nov 26, 2025 · 10 min read
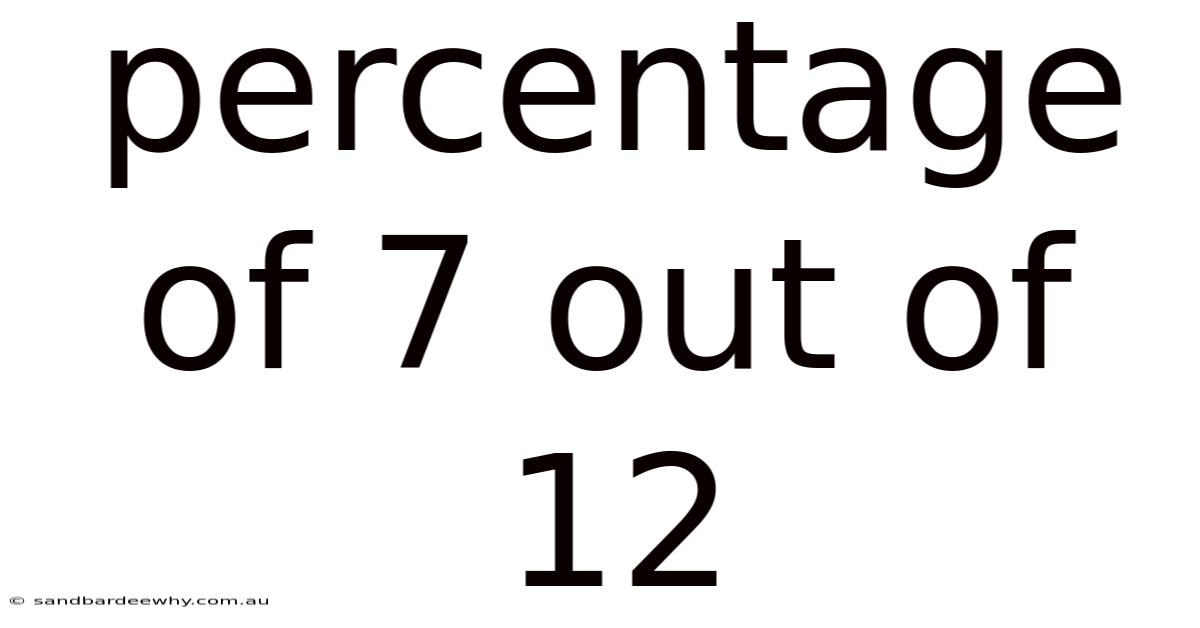
Table of Contents
Imagine you're at a carnival, playing a ring toss game. There are twelve bottles, and you manage to ring seven of them. You might wonder, "How well did I actually do?" or "What's my success rate?" This is where the concept of percentage of 7 out of 12 comes into play. It's a simple calculation that translates your performance into a more understandable and relatable figure.
Understanding percentages is a fundamental skill that extends far beyond carnival games. From calculating discounts while shopping to interpreting statistical data in a report, percentages are a ubiquitous part of modern life. Knowing how to determine the percentage of 7 out of 12 not only helps you assess your hypothetical ring-toss skills but also lays the groundwork for understanding more complex calculations in various fields.
Main Subheading
Percentages provide a standardized way to express proportions and ratios, making it easier to compare different sets of data. In essence, a percentage represents a part of a whole, where the whole is considered to be 100%. It answers the question, "Out of one hundred, how many are we considering?" This makes percentages incredibly useful for analyzing data, understanding statistics, and making informed decisions in everyday situations.
The concept of finding the percentage of 7 out of 12 is a basic application of this principle. It involves expressing the ratio of 7 (the part) to 12 (the whole) as a percentage. This can be applied to countless scenarios, such as calculating your score on a quiz (if you got 7 questions right out of 12), determining the market share of a company (if they sold 7 out of every 12 products), or assessing the efficiency of a process.
Comprehensive Overview
At its core, calculating a percentage involves converting a fraction or a ratio into a value out of 100. The term "percent" literally means "per hundred," derived from the Latin per centum. The symbol "%" is used to denote percentages, making them easily recognizable.
The basic formula for calculating a percentage is:
Percentage = (Part / Whole) * 100
In the specific case of finding the percentage of 7 out of 12, the "part" is 7, and the "whole" is 12. Therefore, the calculation would be:
Percentage = (7 / 12) * 100
When you perform this calculation, you first divide 7 by 12, which results in approximately 0.5833. Then, you multiply this result by 100 to get the percentage, which is approximately 58.33%. So, the percentage of 7 out of 12 is approximately 58.33%.
The beauty of percentages lies in their universality. Regardless of the context, a percentage always represents a proportion out of 100, making it easy to compare and interpret data across different scales. For example, if another person rings 14 out of 24 bottles at the carnival, you can calculate their success rate as (14/24) * 100 = 58.33%. This allows you to directly compare your performance with theirs, even though the total number of bottles they were throwing at was different.
The history of percentages can be traced back to ancient Rome, where taxes were often calculated as a fraction of assets. However, the modern concept of percentages as we know it today developed during the Renaissance, along with the rise of decimal systems and standardized units of measurement. Merchants and traders found percentages particularly useful for calculating profits, interest rates, and taxes. As mathematical notation evolved, the "%" symbol became the standard way to represent percentages, further solidifying their place in commerce and mathematics.
The scientific foundation of percentages rests on the principles of ratios and proportions. A ratio expresses the relative size of two quantities, while a proportion states that two ratios are equal. Percentages are simply a standardized way of expressing ratios as fractions with a denominator of 100. This standardization makes it easier to compare and analyze different datasets. For instance, in scientific research, percentages are often used to express the composition of a mixture, the error rate of an experiment, or the percentage change in a variable over time.
Understanding the underlying concepts of ratios and proportions is essential for mastering percentages. A firm grasp of these principles allows you to apply percentages in various contexts and solve more complex problems. For example, if you know that 30% of a class of students are female and there are 60 students in total, you can use proportions to determine the number of female students: 0.30 = (Number of Female Students) / 60. Solving for the number of female students, you find that there are 18 female students in the class.
Trends and Latest Developments
In today's data-driven world, percentages are more relevant than ever. They are used extensively in business analytics, financial modeling, scientific research, and countless other fields. The ability to calculate and interpret percentages accurately is a crucial skill for anyone working with data.
One significant trend is the increasing use of percentages in data visualization. Charts and graphs often use percentages to represent proportions and distributions, making complex data more accessible to a wider audience. For example, a pie chart might show the market share of different companies, with each slice representing a percentage of the total market. Similarly, a bar graph might show the percentage change in sales over time, allowing viewers to quickly identify trends and patterns.
Another trend is the use of percentages in machine learning and artificial intelligence. Many machine learning algorithms rely on percentages to assess the accuracy of their predictions. For example, the accuracy of a classification model might be expressed as the percentage of correctly classified instances. Additionally, percentages are used to measure the confidence level of a prediction, providing insights into the reliability of the model's output.
According to recent surveys, a significant percentage of adults struggle with basic mathematical concepts, including percentages. This highlights the importance of improving numeracy skills and providing accessible educational resources. Many online tools and educational platforms offer interactive lessons and practice exercises to help people master percentages and other essential math skills.
Professional insights suggest that a deeper understanding of percentages can lead to better decision-making in various contexts. For example, in finance, understanding compound interest and percentage returns can help investors make informed choices about their investments. In marketing, analyzing conversion rates and customer acquisition costs as percentages can help businesses optimize their strategies and improve their return on investment.
Moreover, the rise of big data and data analytics has further amplified the importance of percentages. As organizations collect and analyze vast amounts of data, the ability to extract meaningful insights using percentages becomes increasingly valuable. Data analysts and scientists use percentages to summarize data, identify patterns, and communicate findings to stakeholders.
Tips and Expert Advice
Calculating the percentage of 7 out of 12 is a straightforward process, but there are some tips and tricks that can help you perform the calculation more efficiently and accurately.
First, it's important to understand the context of the problem. Are you trying to calculate your score on a test, determine the market share of a company, or assess the efficiency of a process? Understanding the context will help you interpret the result and make informed decisions. For example, if you're calculating your score on a test, a percentage of 58.33% might indicate that you need to study harder for the next test. However, if you're determining the market share of a company, a percentage of 58.33% might indicate that the company is a major player in the market.
Second, it's helpful to memorize some common percentage equivalents. For example, knowing that 1/2 is equal to 50%, 1/4 is equal to 25%, and 1/5 is equal to 20% can help you estimate percentages quickly and easily. In the case of percentage of 7 out of 12, recognizing that 6/12 is 50% can give you a starting point for estimating the final result. Since 7/12 is slightly more than 6/12, you know that the percentage will be slightly more than 50%.
Third, it's useful to use a calculator or spreadsheet program to perform the calculation. While it's important to understand the underlying principles of percentages, using technology can help you avoid errors and save time. Most calculators have a percentage function that allows you to calculate percentages directly. Alternatively, you can use a spreadsheet program like Microsoft Excel or Google Sheets to perform the calculation. In Excel, you can simply enter the formula "=7/12*100" to calculate the percentage of 7 out of 12.
Fourth, it's important to double-check your work to ensure that you haven't made any errors. One common mistake is to divide the whole by the part instead of dividing the part by the whole. Another common mistake is to forget to multiply the result by 100. To avoid these errors, always double-check your calculations and make sure that your answer makes sense in the context of the problem.
Finally, it's helpful to practice calculating percentages regularly. The more you practice, the more comfortable you'll become with the concept and the more easily you'll be able to apply it in different situations. There are many online resources and practice exercises that can help you improve your percentage skills.
FAQ
Q: What is a percentage? A: A percentage is a way of expressing a number as a fraction of 100. It represents a part of a whole, where the whole is considered to be 100%.
Q: How do I calculate a percentage? A: To calculate a percentage, divide the part by the whole and multiply the result by 100. The formula is: Percentage = (Part / Whole) * 100.
Q: What is the percentage of 7 out of 12? A: The percentage of 7 out of 12 is approximately 58.33%. This is calculated as (7 / 12) * 100.
Q: Why are percentages useful? A: Percentages provide a standardized way to express proportions and ratios, making it easier to compare different sets of data. They are used in various fields, including business, finance, science, and education.
Q: Where can I use percentages in real life? A: Percentages are used in many real-life situations, such as calculating discounts while shopping, determining your score on a test, understanding statistics in a report, and making informed decisions in everyday situations.
Conclusion
In summary, understanding how to calculate the percentage of 7 out of 12 is a valuable skill that has practical applications in various aspects of life. It's a fundamental concept in mathematics that helps us express proportions and ratios in a standardized and easily understandable way. By dividing the part (7) by the whole (12) and multiplying by 100, we arrive at approximately 58.33%, which represents the proportion of 7 out of 12.
Whether you're assessing your performance in a game, analyzing data in a report, or making informed decisions in your personal or professional life, the ability to calculate and interpret percentages is essential. So, take the time to practice and master this skill, and you'll be well-equipped to tackle a wide range of numerical challenges.
Now that you understand the process, try calculating the percentage of 7 out of 12 in different scenarios. Share your examples and any questions you may have in the comments below! Let's continue the conversation and deepen our understanding of this essential mathematical concept.
Latest Posts
Latest Posts
-
Definition Of Plunder In The Bible
Nov 26, 2025
-
Nj Real Estate License Exam Practice
Nov 26, 2025
-
Who Is Moishe The Beadle In Night
Nov 26, 2025
-
Percentage Of 7 Out Of 12
Nov 26, 2025
-
The Counter Reformation Was A Religious And Political Movement That
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about Percentage Of 7 Out Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.