What Is 2 To The Power Of 5
sandbardeewhy
Nov 24, 2025 · 13 min read
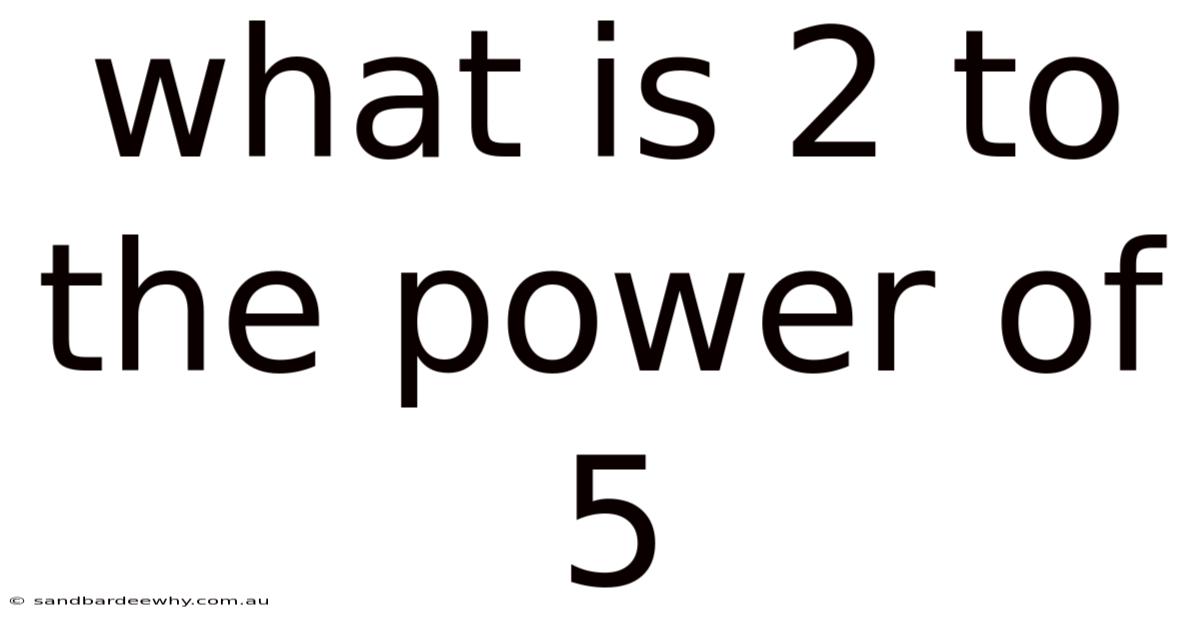
Table of Contents
Imagine you're at a bake sale, and your mom decides to bake cookies for everyone. She starts with two cookies. Then, she doubles it to four, then again to eight. She keeps doubling the number of cookies five times in a row. How many cookies does she end up baking?
Or, perhaps you are thinking about computer storage. Computers use a binary system, based on powers of 2. A kilobyte is 2 to the power of 10 bytes, and then megabytes, gigabytes, and terabytes all are based on successive powers of 2. Understanding powers of 2 helps to grasp how digital information is stored and processed. So, let’s understand a common term: what is 2 to the power of 5?
Understanding Powers: What is 2 to the Power of 5?
In mathematics, the "power" of a number signifies how many times that number is multiplied by itself. When we talk about 2 to the power of 5, we mean 2 multiplied by itself five times. This mathematical operation is a fundamental concept in algebra and arithmetic and is written as 2^5. In simpler terms, it's 2 × 2 × 2 × 2 × 2.
To really understand what 2 to the power of 5 means, it's helpful to break down the concept of exponents. The expression "2 to the power of 5" consists of two main parts: the base (2) and the exponent (5). The base is the number that is being multiplied, and the exponent indicates how many times the base is multiplied by itself. Exponents offer a shorthand way to represent repeated multiplication, making it easier to work with large numbers and complex equations. In this context, 2 is the base and 5 is the exponent, so we are multiplying 2 by itself five times.
The concept of powers is essential not just for simple arithmetic but also for more advanced mathematical topics such as polynomial functions, exponential growth, and calculus. For example, understanding exponential growth can help you predict population increases or the spread of viruses. Powers also play a crucial role in scientific notation, which is used to express very large or very small numbers in a concise and manageable format. For instance, the speed of light is approximately 3 x 10^8 meters per second, where 10^8 means 10 to the power of 8. In computer science, powers of 2 are particularly important. The binary system, which is the foundation of how computers store and process information, is based on powers of 2. Each digit in a binary number represents a power of 2, starting from 2^0 on the rightmost digit.
The origins of exponents and powers can be traced back to ancient civilizations. Early mathematicians in Mesopotamia and Egypt developed systems for expressing and working with powers, primarily for calculations related to astronomy, land surveying, and commerce. These early notations were somewhat different from modern notation but served a similar purpose: to simplify complex calculations and represent repeated multiplication more efficiently. Over time, mathematicians from various cultures, including Greek and Indian scholars, contributed to the development and refinement of exponential notation and the understanding of its properties.
One of the most significant advancements in the understanding of powers came with the development of algebra. As algebraic notation became more standardized, mathematicians were able to generalize the concept of exponents and explore their properties in more abstract and theoretical contexts. This led to the discovery of important rules and identities, such as the power rule (a^m * a^n = a^(m+n)) and the quotient rule (a^m / a^n = a^(m-n)), which are fundamental to algebraic manipulation and problem-solving.
Comprehensive Overview of Exponents and Powers
At its core, the concept of "to the power of" is about repeated multiplication. The expression a^n* (read as "a to the power of n") means multiplying a by itself n times. For example, 3^4 is 3 × 3 × 3 × 3, which equals 81. Understanding this basic principle is crucial for grasping more complex mathematical concepts.
The concept of exponents and powers is a cornerstone of algebra and plays a vital role in many scientific and engineering disciplines. Exponents provide a succinct way to express repeated multiplication, which is essential for calculations involving large or small numbers, as well as for modeling various phenomena in physics, biology, and computer science. A thorough understanding of exponents involves grasping the fundamental rules that govern their behavior, such as the product rule, quotient rule, power rule, and the rules for dealing with negative and fractional exponents.
The Base and the Exponent
In the expression a^n*, "a" is the base, and "n" is the exponent (or power). The base is the number being multiplied, and the exponent indicates how many times the base is multiplied by itself. For instance, in 5^3, 5 is the base, and 3 is the exponent.
Rules of Exponents
There are several fundamental rules that govern how exponents work, which are essential for simplifying expressions and solving equations:
- Product Rule: When multiplying two powers with the same base, add the exponents.
- a^m * a^n = a^(m+n)
- Example: 2^3 * 2^2 = 2^(3+2) = 2^5 = 32
- Quotient Rule: When dividing two powers with the same base, subtract the exponents.
- a^m / a^n = a^(m-n)
- Example: 3^5 / 3^2 = 3^(5-2) = 3^3 = 27
- Power Rule: When raising a power to another power, multiply the exponents.
- (a^m)^n = a^(m*n)
- Example: (4^2)^3 = 4^(2*3) = 4^6 = 4096
- Zero Exponent: Any number (except zero) raised to the power of 0 is 1.
- a^0 = 1 (where a ≠ 0)
- Example: 7^0 = 1
- Negative Exponent: A number raised to a negative exponent is equal to the reciprocal of the number raised to the positive exponent.
- a^-n = 1 / a^n
- Example: 2^-3 = 1 / 2^3 = 1/8 = 0.125
- Fractional Exponent: A fractional exponent represents a root. For example, a^(1/n) is the nth root of a.
- a^(m/n) = (n√a)^m
- Example: 9^(1/2) = √9 = 3
History and Evolution of Exponents
The concept of exponents has ancient roots, with early notations appearing in Babylonian mathematics around 2000 BCE. However, these notations were primarily used to express squares and cubes and did not generalize to higher powers. The systematic use of exponents began to develop more formally in the 16th and 17th centuries.
- Early Notations: Ancient civilizations, including the Babylonians and Greeks, used geometric representations and specific symbols to denote squares and cubes.
- Medieval Period: During the medieval period, mathematicians like Nicolas Chuquet began to use notations that resemble modern exponents, but they were not yet standardized.
- 17th Century: René Descartes introduced the modern notation of using superscripts to denote exponents in his work La Géométrie (1637), which helped to standardize the notation and make it more widely adopted.
- Later Developments: Over time, mathematicians refined the understanding of exponents, extending them to include negative, fractional, and complex exponents, which greatly expanded their applicability in various fields of mathematics and science.
Trends and Latest Developments
Recent trends in the use of exponents and powers are closely linked to advances in technology and data science. The exponential growth of computing power, as described by Moore's Law, has driven the need for efficient algorithms and data structures that can handle increasingly large datasets. In data analysis, exponential functions are used to model various phenomena, such as the spread of information in social networks or the decay of radioactive substances.
One significant trend is the application of exponential functions in machine learning, particularly in neural networks. Activation functions like the exponential linear unit (ELU) are used to introduce non-linearity into the model, enabling it to learn complex patterns in the data. Additionally, the Softmax function, which involves exponentiation, is commonly used in multi-class classification problems to convert raw scores into probabilities.
In finance, exponential functions are used to model compound interest and the growth of investments over time. The formula for compound interest involves raising the interest rate plus one to the power of the number of compounding periods, which highlights the significant impact of exponential growth on long-term investment returns.
According to a recent report by McKinsey, the volume of data generated globally is expected to continue growing exponentially, doubling approximately every two years. This trend underscores the importance of understanding and utilizing exponential functions to analyze and interpret large datasets effectively.
Popular Opinions and Insights
Experts in mathematics and computer science emphasize the importance of mastering exponents for various reasons. Dr. Susan Landau, a renowned mathematician and computer scientist, notes that "a solid understanding of exponents is crucial for anyone working with algorithms, data structures, or cryptography." She adds that many efficient algorithms rely on exponential functions to achieve optimal performance.
Moreover, educators highlight the importance of teaching exponents effectively from an early age. A study published in the Journal for Research in Mathematics Education found that students who develop a strong foundation in exponents and powers are more likely to succeed in advanced mathematics courses. The study suggests that using visual aids and real-world examples can help students grasp the abstract concepts more easily.
Tips and Expert Advice
Working with exponents can sometimes be tricky, especially when dealing with complex expressions or large numbers. Here are some tips and expert advice to help you master exponents:
Simplify Expressions
Before performing any calculations, always try to simplify the expression first. Look for opportunities to apply the rules of exponents to combine like terms or reduce the expression to its simplest form. For example, if you have an expression like (2^3 * 2^2) / 2^4, you can simplify it by first adding the exponents in the numerator (2^(3+2) = 2^5) and then subtracting the exponent in the denominator (2^(5-4) = 2^1 = 2).
Simplifying expressions not only makes the calculations easier but also reduces the likelihood of making errors. When dealing with complex expressions, break them down into smaller, more manageable parts and apply the rules of exponents step by step. This approach can help you avoid confusion and ensure that you arrive at the correct answer.
Use Scientific Notation
When dealing with very large or very small numbers, using scientific notation can make the calculations much easier. Scientific notation expresses numbers as a product of a number between 1 and 10 and a power of 10. For example, the number 3,000,000 can be written as 3 x 10^6 in scientific notation. This format is particularly useful when performing calculations involving exponents because it allows you to easily combine the powers of 10.
Scientific notation is widely used in scientific and engineering fields to represent measurements and quantities that span a wide range of magnitudes. By using scientific notation, you can avoid writing long strings of zeros and simplify the process of performing calculations with these numbers. Additionally, scientific notation helps to maintain precision and accuracy, as it allows you to specify the number of significant figures in a measurement.
Double-Check Your Work
One of the most common mistakes when working with exponents is making errors in the arithmetic. Always double-check your work to ensure that you have correctly applied the rules of exponents and performed the calculations accurately. Use a calculator to verify your results, especially when dealing with complex expressions or large numbers.
Additionally, pay close attention to the signs of the exponents and the order of operations. A simple mistake in the sign of an exponent or the order in which you perform the calculations can lead to a completely different answer. By being careful and thorough in your work, you can minimize the risk of making errors and ensure that you arrive at the correct solution.
Practice Regularly
Like any mathematical skill, mastering exponents requires regular practice. Work through a variety of problems involving exponents to reinforce your understanding of the rules and concepts. Start with simple problems and gradually work your way up to more complex ones. The more you practice, the more confident and proficient you will become in working with exponents.
There are many resources available to help you practice exponents, including textbooks, online tutorials, and practice worksheets. Take advantage of these resources to supplement your learning and reinforce your understanding of the material. Additionally, consider working with a tutor or study group to get personalized feedback and support.
Use Real-World Examples
Connecting exponents to real-world examples can help you better understand and appreciate their relevance. Look for opportunities to apply exponents to solve practical problems in areas such as finance, science, and engineering. For example, you can use exponents to calculate compound interest, model population growth, or analyze the decay of radioactive substances.
By seeing how exponents are used in real-world applications, you can gain a deeper understanding of their significance and develop a greater appreciation for their role in mathematics and science. Additionally, using real-world examples can make learning exponents more engaging and enjoyable.
FAQ about Exponents
Q: What does a negative exponent mean?
A: A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example, a^-n = 1 / a^n. So, 2^-2 = 1 / 2^2 = 1/4.
Q: How do you simplify expressions with exponents?
A: To simplify expressions with exponents, apply the rules of exponents, such as the product rule, quotient rule, and power rule. Combine like terms, reduce fractions, and simplify any numerical calculations.
Q: What is the difference between 2^0 and 0^2?
A: Any non-zero number raised to the power of 0 is 1, so 2^0 = 1. However, 0 raised to any positive power is 0, so 0^2 = 0.
Q: Can exponents be fractions?
A: Yes, exponents can be fractions. A fractional exponent represents a root. For example, a^(1/n) is the nth root of a. So, 4^(1/2) = √4 = 2.
Q: How are exponents used in science and engineering?
A: Exponents are used extensively in science and engineering to represent and manipulate very large or very small numbers, model exponential growth and decay, and solve complex equations in various fields such as physics, chemistry, and computer science.
Conclusion
So, what is 2 to the power of 5? It's 2 multiplied by itself five times, which equals 32. Understanding exponents is not just about crunching numbers; it's about grasping a fundamental concept that underpins much of mathematics and its applications in the real world. From baking cookies to understanding computer storage, exponents are everywhere.
Now that you have a solid understanding of exponents, it's time to put your knowledge to the test. Try solving some practice problems involving exponents, explore real-world applications of exponential functions, and continue to deepen your understanding of this important mathematical concept. Share this article with friends and colleagues who might benefit from learning more about exponents and powers.
Latest Posts
Latest Posts
-
Life Expectancy Of A Snapping Turtle
Nov 24, 2025
-
What Is A 35 Out Of 50
Nov 24, 2025
-
Songs That Represent The 7th Amendment
Nov 24, 2025
-
What Is 2 To The Power Of 5
Nov 24, 2025
-
How Far Is The Moon From The Sun
Nov 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 To The Power Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.