What Is 3 Percent Of 15
sandbardeewhy
Nov 23, 2025 · 11 min read
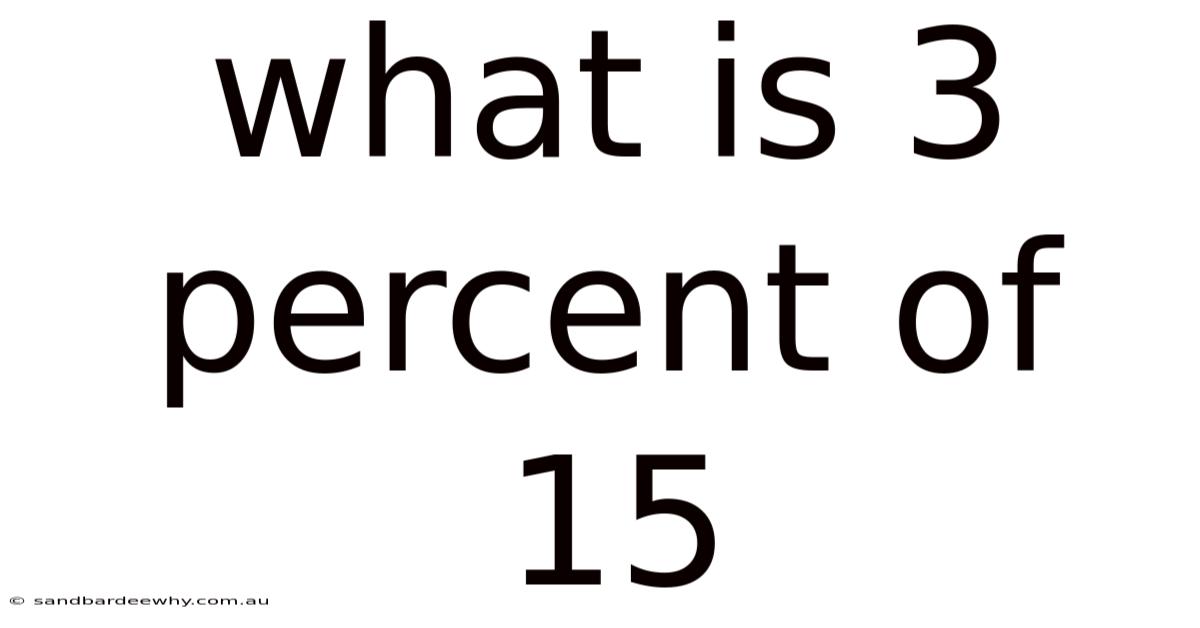
Table of Contents
Imagine you're at your favorite coffee shop, and the barista tells you that you'll get a 3 percent discount on your usual $15 order. It sounds like a sweet deal, but how much will you actually save? Or picture this: you're about to invest $15,000 in a promising startup, and an advisor mentions that they project a 3 percent growth in the first year. How much can you expect your investment to increase?
Understanding how to calculate percentages is a fundamental life skill that pops up in various everyday scenarios. From discounts and tips to financial planning and data analysis, knowing how to quickly and accurately find a percentage of a number can save you time, money, and a whole lot of confusion. In this article, we'll break down the simple steps to calculate 3 percent of 15, explore why this seemingly small calculation matters, and provide practical tips to make you a percentage pro in no time.
Understanding the Basics of Percentage Calculation
The concept of percentage is deeply rooted in mathematics and is used to express a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." This simple yet powerful idea has become an indispensable tool in various fields, from finance and statistics to everyday shopping. Understanding the foundation of percentage calculation is essential before diving into more complex problems.
What is a Percentage?
A percentage is a way of expressing a ratio or fraction with a denominator of 100. It tells you how many parts of a whole you have if the whole is divided into 100 equal parts. For example, if you score 80 out of 100 on a test, you scored 80 percent (80%) – meaning you got 80 parts right out of 100. Percentages make it easier to compare different fractions or ratios, as they all have a common base of 100.
The Formula for Calculating Percentage
The basic formula to calculate a percentage is quite straightforward:
Percentage = (Part / Whole) * 100
Where:
- Part is the specific quantity you are interested in.
- Whole is the total or the reference value.
For example, if you want to find what percentage 20 is of 50, you would use the formula like this:
Percentage = (20 / 50) * 100 = 40%
This means that 20 is 40% of 50. Understanding this formula is the cornerstone of all percentage calculations.
How to Find a Percentage of a Number
Sometimes, you need to find a specific percentage of a given number. This is common in situations like calculating discounts, tips, or interest rates. The formula for finding a percentage of a number is:
Value = (Percentage / 100) * Total Number
Here:
- Percentage is the percentage you want to find.
- Total Number is the whole quantity.
For example, if you want to find 25% of 80, you would calculate it as:
Value = (25 / 100) * 80 = 20
This means that 25% of 80 is 20.
Why Percentages Matter
Percentages are incredibly useful because they provide a standardized way to compare and understand proportions. Without percentages, comparing fractions with different denominators would be much more complicated. For instance, it's easier to grasp that 75% is larger than 60% than it is to compare 3/4 and 3/5 directly.
Percentages also simplify complex data and make it more accessible. Imagine reading a financial report without percentages; it would be filled with complicated fractions and ratios, making it difficult to quickly understand the key takeaways. Percentages allow us to easily interpret and communicate information, making them an essential part of modern communication and analysis.
Real-World Applications of Percentages
The applications of percentages are vast and varied. Here are a few examples:
- Finance: Calculating interest rates on loans, returns on investments, and profit margins in business.
- Retail: Determining discounts on products, sales tax, and markup percentages.
- Statistics: Analyzing survey results, calculating growth rates, and understanding demographic data.
- Health: Monitoring changes in weight, body fat percentage, and medication dosages.
- Education: Grading exams, calculating student performance, and comparing test scores.
In each of these areas, percentages provide a clear and concise way to understand and communicate quantitative information.
Step-by-Step Guide to Calculating 3 Percent of 15
Now that we have a good grasp of the fundamentals of percentage calculations, let's dive into our specific problem: calculating 3 percent of 15. We will break down the process into simple, manageable steps.
Step 1: Convert the Percentage to a Decimal
The first step in finding a percentage of a number is to convert the percentage into a decimal. To do this, you divide the percentage by 100. In our case, we want to find 3 percent, so we divide 3 by 100:
3 / 100 = 0.03
So, 3 percent is equivalent to 0.03 in decimal form. This conversion is crucial because it allows us to easily multiply by the total number to find the desired value.
Step 2: Multiply the Decimal by the Total Number
Next, multiply the decimal obtained in Step 1 by the total number. In this case, we want to find 3 percent of 15, so we multiply 0.03 by 15:
- 03 * 15 = 0.45
Therefore, 3 percent of 15 is 0.45.
Alternative Method: Using Fractions
Another way to calculate 3 percent of 15 is by using fractions. This method can be particularly useful if you prefer working with fractions or want to understand the underlying mathematical relationship more deeply.
-
Express the Percentage as a Fraction: Convert 3 percent into a fraction by placing it over 100:
3% = 3/100
-
Multiply the Fraction by the Total Number: Multiply the fraction (3/100) by the total number (15):
(3/100) * 15 = (3 * 15) / 100 = 45 / 100
-
Simplify the Fraction: Simplify the fraction 45/100. Both 45 and 100 are divisible by 5:
45/100 = 9/20
-
Convert the Fraction to a Decimal (Optional): If desired, convert the fraction 9/20 to a decimal by dividing 9 by 20:
9 / 20 = 0.45
As you can see, both methods—using decimals and using fractions—arrive at the same answer: 3 percent of 15 is 0.45.
Practical Example: Calculating a Discount
Let's say you want to buy an item that costs $15, and you have a coupon for a 3 percent discount. To find out how much money you will save, you need to calculate 3 percent of 15.
Using the method we discussed:
- Convert 3 percent to a decimal: 3 / 100 = 0.03
- Multiply the decimal by the total price: 0.03 * 15 = 0.45
So, you will save $0.45 on your purchase. The discounted price will be $15 - $0.45 = $14.55.
Tips for Quick Mental Calculations
Calculating percentages mentally can be a valuable skill in many situations. Here are a few tips to help you calculate 3 percent of 15 and other similar percentages quickly:
-
Break It Down: Instead of calculating 3 percent directly, you can find 1 percent first and then multiply by 3. To find 1 percent of 15, divide 15 by 100:
15 / 100 = 0.15
Then, multiply 0.15 by 3:
- 15 * 3 = 0.45
-
Use Round Numbers: If you're struggling with the exact number, round it to the nearest whole number or easy-to-work-with value. For instance, you could think of 3 percent of 15 as approximately 3 percent of 15. This provides a quick estimate, which you can then adjust if necessary.
-
Practice Regularly: Like any skill, mental math improves with practice. Try calculating percentages in everyday situations, such as when shopping or dining out. Over time, you'll become more comfortable and efficient.
Common Mistakes to Avoid
While calculating percentages is relatively straightforward, there are a few common mistakes that people often make. Being aware of these pitfalls can help you avoid errors and ensure accurate calculations.
Misunderstanding the Base Number
One of the most common mistakes is applying the percentage to the wrong base number. Always make sure you are clear about what the "whole" is in your calculation. For instance, if you are calculating a discount, ensure you are applying the percentage to the original price, not a previously discounted price.
Forgetting to Convert Percentage to Decimal or Fraction
Another frequent error is forgetting to convert the percentage to a decimal or fraction before performing the calculation. Remember that you need to divide the percentage by 100 to get the decimal form or express it as a fraction over 100. Failing to do so will result in a significantly incorrect answer.
Rounding Errors
Rounding errors can also lead to inaccuracies, especially when dealing with multiple steps in a calculation. It's best to keep as many decimal places as possible throughout the calculation and only round the final answer to the desired level of precision.
Misinterpreting the Question
Sometimes, the wording of the question can be confusing. Make sure you understand exactly what is being asked. For example, are you being asked to find a percentage of a number, or are you being asked to find what percentage one number is of another?
Trends and Latest Developments
In today's data-driven world, the application of percentages is more relevant than ever. Here are some of the latest trends and developments related to percentage calculations:
Data Visualization
Data visualization tools often use percentages to represent data in a clear and understandable way. Charts, graphs, and infographics frequently display percentages to show proportions and distributions, making complex data more accessible to a broader audience. This trend is particularly evident in business analytics, marketing, and scientific research.
Financial Technology (FinTech)
FinTech companies rely heavily on percentage calculations for various applications, such as calculating interest rates on loans, returns on investments, and risk assessments. Advanced algorithms and machine learning models use percentages to analyze financial data and provide personalized recommendations to users.
E-commerce and Retail
In the e-commerce and retail sectors, percentages are used extensively for pricing strategies, discount offers, and sales analysis. Retailers use percentages to calculate profit margins, markdown prices, and the effectiveness of promotional campaigns. Furthermore, customer analytics often involve calculating percentages to understand purchasing patterns and customer behavior.
Educational Tools
Educational platforms are increasingly incorporating interactive tools and simulations to teach percentage calculations. These resources help students grasp the concept of percentages in a more engaging and practical way. Gamified learning experiences and real-world scenarios are used to make learning about percentages more fun and relevant.
Tips and Expert Advice
To become truly proficient in percentage calculations, consider the following tips and expert advice:
Practice Regularly
Consistent practice is key to mastering any mathematical skill. Incorporate percentage calculations into your daily routine, whether it's calculating tips at a restaurant or estimating discounts while shopping. The more you practice, the more comfortable and confident you'll become.
Understand the Context
Always take the time to understand the context of the problem. What are you trying to calculate? What are the relevant numbers? By understanding the context, you can avoid common mistakes and ensure that you are applying the correct formulas.
Use Technology Wisely
While it's important to understand the fundamentals of percentage calculations, don't hesitate to use technology to your advantage. Calculators, spreadsheets, and online tools can help you perform complex calculations quickly and accurately. However, make sure you understand the underlying math, so you can verify the results and avoid relying solely on technology.
Break Down Complex Problems
When faced with a complex problem involving percentages, break it down into smaller, more manageable steps. This will make the problem less intimidating and reduce the likelihood of errors. For example, if you need to calculate a series of discounts, calculate each discount separately before combining them.
Seek Feedback and Learn from Mistakes
Don't be afraid to ask for help or seek feedback from others. If you're struggling with a particular concept, ask a teacher, tutor, or colleague for assistance. Additionally, take the time to analyze your mistakes and learn from them. Understanding why you made an error can help you avoid making the same mistake in the future.
FAQ
Q: What is the formula for calculating a percentage of a number?
A: The formula is: Value = (Percentage / 100) * Total Number.
Q: How do I convert a percentage to a decimal?
A: Divide the percentage by 100. For example, 25% = 25 / 100 = 0.25.
Q: Can you use fractions to calculate percentages?
A: Yes, you can convert the percentage to a fraction by placing it over 100 and then multiply the fraction by the total number.
Q: What is 10 percent of 50?
A: 10 percent of 50 is (10 / 100) * 50 = 5.
Q: How do I calculate a percentage increase?
A: To calculate a percentage increase, use the formula: ((New Value - Original Value) / Original Value) * 100.
Conclusion
Calculating 3 percent of 15 is a simple yet essential mathematical skill with numerous real-world applications. By converting the percentage to a decimal or fraction and multiplying it by the total number, you can easily find the desired value. Whether you're calculating discounts, tips, or financial returns, understanding how to work with percentages is a valuable asset. By following the steps outlined in this article, avoiding common mistakes, and practicing regularly, you can become proficient in percentage calculations and confidently apply this skill in various aspects of your life.
Ready to put your new skills to the test? Try calculating percentages in your everyday activities, such as when shopping, dining out, or managing your finances. Share your experiences and insights in the comments below, and let's continue to explore the fascinating world of mathematics together!
Latest Posts
Latest Posts
-
20 Gallons Is How Many Quarts
Nov 23, 2025
-
What Is 3 Percent Of 15
Nov 23, 2025
-
How To Find The Domain Of A Log Function
Nov 23, 2025
-
Receptors For Hearing Are Located In The
Nov 23, 2025
-
Is The Square Root Of 3 A Rational Number
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.