What Is 4 To The Power Of 3
sandbardeewhy
Nov 22, 2025 · 9 min read
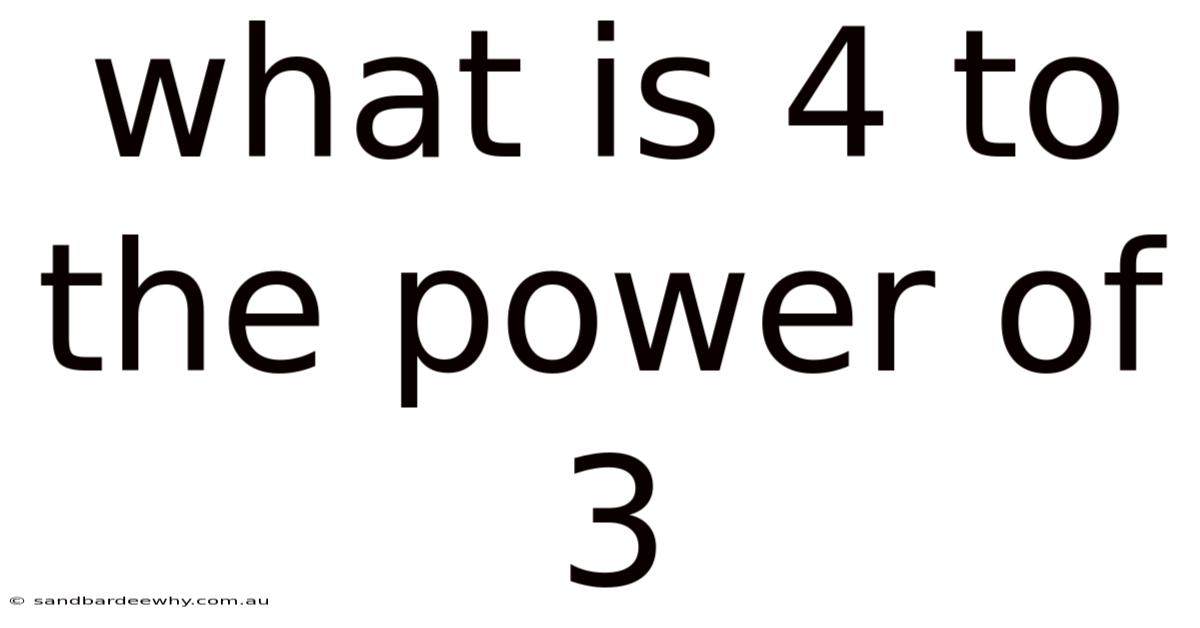
Table of Contents
Imagine you're stacking building blocks. You start with one block, then you build a square of four blocks, then you build up from that square, creating a cube. That cube represents 4 to the power of 3, or 4 cubed. It's a simple idea with profound applications, extending far beyond children's toys into the realms of science, finance, and even art.
Whether you're calculating the volume of a room, understanding exponential growth, or simply brushing up on your math skills, knowing "what is 4 to the power of 3" is a surprisingly useful piece of knowledge. It's a fundamental concept in mathematics that unlocks understanding of more complex ideas and helps us to make sense of the world around us.
Understanding Exponents: What is 4 to the Power of 3?
At its core, 4 to the power of 3, often written as 4³, represents repeated multiplication. The "4" is the base, and the "3" is the exponent or power. The exponent tells you how many times to multiply the base by itself. In this case, 4³ means 4 multiplied by itself three times: 4 x 4 x 4. Understanding this fundamental definition is the key to unlocking the meaning of exponents in mathematics.
Calculating 4³ is straightforward. First, multiply 4 by 4, which equals 16. Then, multiply that result (16) by 4 again. The final answer is 64. Therefore, 4 to the power of 3 equals 64. This simple calculation demonstrates the core principle of exponentiation: a concise way to express repeated multiplication.
A Comprehensive Overview of Exponentiation
Exponentiation, also known as raising to a power, is a mathematical operation involving two numbers: the base and the exponent. The exponent indicates how many times the base is multiplied by itself. This concept extends far beyond simple whole numbers, encompassing fractions, decimals, negative numbers, and even variables.
The history of exponentiation can be traced back to ancient civilizations. Early forms of mathematical notation, developed by the Babylonians and Egyptians, contained elements that resembled exponents. However, the modern notation we use today, with a superscript to denote the exponent, was gradually developed over centuries, solidifying in the 17th century with the work of mathematicians like René Descartes.
Mathematically, exponentiation can be formally defined as follows:
-
For any real number a (the base) and any positive integer n (the exponent):
a<sup>n</sup> = a × a × a × ... × a (n times)
-
When the exponent is 0:
a<sup>0</sup> = 1 (provided a is not 0)
-
When the exponent is a negative integer:
a<sup>-n</sup> = 1 / a<sup>n</sup>
-
When the exponent is a fraction (rational number):
a<sup>m/n</sup> = <sup>n</sup>√a<sup>m</sup> (the n-th root of a raised to the power of m)
These definitions lay the foundation for understanding how exponents work across different types of numbers. The properties of exponents, such as the product of powers rule (a<sup>m</sup> * a<sup>n</sup> = a<sup>m+n</sup>) and the power of a power rule ((a<sup>m</sup>)<sup>n</sup> = a<sup>m*n</sup>), are crucial for simplifying expressions and solving equations involving exponents. These rules streamline calculations and provide a framework for manipulating exponential expressions with efficiency.
Beyond basic arithmetic, exponentiation plays a critical role in various branches of mathematics, including algebra, calculus, and number theory. In algebra, exponential functions are used to model growth and decay processes. In calculus, derivatives and integrals of exponential functions are essential for solving problems in physics and engineering. In number theory, exponents are used to study prime numbers and other fundamental properties of integers.
The power of exponentiation also shines in scientific notation, a standardized way to express very large or very small numbers. Scientific notation uses powers of 10 to represent numbers concisely. For example, the number 3,000,000,000 can be written as 3 x 10<sup>9</sup>. This notation simplifies calculations and makes it easier to compare numbers of vastly different magnitudes. Understanding exponents is, therefore, essential for navigating many scientific disciplines.
Trends and Latest Developments in Exponentiation
While the basic principles of exponentiation remain constant, ongoing research continues to explore its applications in new and exciting ways. One significant trend is the use of exponentiation in cryptography. Many modern encryption algorithms rely on the computational difficulty of finding the prime factors of large numbers, a process deeply intertwined with exponential calculations. The RSA algorithm, a widely used public-key cryptosystem, leverages the properties of exponentiation to secure sensitive data transmitted over the internet.
Another area of active development is the study of fractional exponents and their connection to fractals. Fractals are complex geometric shapes that exhibit self-similarity at different scales. Fractional exponents play a crucial role in defining the dimensions of fractals, providing a mathematical framework for understanding their intricate structures. This interdisciplinary field connects mathematics, computer science, and art, demonstrating the far-reaching applications of exponentiation.
Furthermore, advancements in computing technology have enabled researchers to perform complex calculations involving extremely large exponents. These calculations are used in various fields, including climate modeling, financial analysis, and particle physics. High-performance computing clusters and specialized algorithms are essential tools for tackling these computationally intensive problems, pushing the boundaries of what is possible with exponentiation.
In education, there's a growing emphasis on teaching exponents conceptually, rather than just memorizing rules. Interactive simulations and visual aids are increasingly used to help students understand the underlying principles of exponentiation. This approach fosters a deeper understanding of the subject and encourages students to explore its applications in real-world contexts. Educational platforms often incorporate games and challenges that make learning about exponents more engaging and enjoyable.
Tips and Expert Advice for Mastering Exponents
Understanding exponents is crucial for success in mathematics and related fields. Here's some expert advice to help you master this fundamental concept:
-
Solidify the Basics: Ensure you have a firm grasp of the fundamental definition of exponents: repeated multiplication. Understand that a<sup>n</sup> means multiplying a by itself n times. Practice with simple examples like 2², 3³, and 5² to reinforce this understanding. Also, make sure to know that any number to the power of zero (except zero itself) equals one. A clear understanding of these basics is the bedrock upon which more complex concepts are built.
-
Memorize the Rules of Exponents: Commit to memory the key rules of exponents, such as the product of powers rule (a<sup>m</sup> * a<sup>n</sup> = a<sup>m+n</sup>), the quotient of powers rule (a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>), and the power of a power rule ((a<sup>m</sup>)<sup>n</sup> = a<sup>m*n</sup>). Practice applying these rules to simplify expressions and solve equations. Flashcards, online quizzes, and consistent practice problems are excellent ways to solidify your knowledge of these rules.
-
Work Through Practice Problems: The best way to master exponents is through practice. Start with simple problems and gradually increase the difficulty. Focus on understanding the why behind each step, rather than just memorizing the process. Solve a variety of problems involving different types of exponents, including integers, fractions, and negative numbers. Seek out online resources, textbooks, and worksheets to find a wealth of practice problems.
-
Visualize Exponents: For some learners, visualizing exponents can aid in understanding. Consider how squares and cubes relate to exponents of 2 and 3, respectively. Think about how exponential growth manifests in real-world scenarios, such as population growth or compound interest. Creating mental images or diagrams can make abstract concepts more concrete and relatable.
-
Relate Exponents to Real-World Applications: Understanding how exponents are used in real-world scenarios can make them more relevant and engaging. Explore examples in finance (compound interest), science (exponential decay of radioactive materials), and computer science (algorithm complexity). Seeing the practical applications of exponents can increase your motivation to learn and deepen your understanding.
-
Use Online Resources and Tools: Take advantage of the many online resources available to help you learn about exponents. Websites like Khan Academy, Wolfram Alpha, and Mathway offer tutorials, practice problems, and calculators to assist you in your learning journey. Explore interactive simulations and games that make learning about exponents more fun and engaging.
-
Seek Help When Needed: Don't hesitate to ask for help when you're struggling with exponents. Talk to your teacher, classmates, or a tutor. Explain your difficulties clearly and ask specific questions. Collaboration and discussion can often lead to new insights and a deeper understanding of the subject. Online forums and communities can also provide valuable support and guidance.
FAQ: Frequently Asked Questions About Exponents
Q: What does it mean when an exponent is negative?
A: A negative exponent indicates the reciprocal of the base raised to the positive version of that exponent. For example, a<sup>-n</sup> = 1 / a<sup>n</sup>. So, 2<sup>-2</sup> = 1 / 2<sup>2</sup> = 1 / 4.
Q: What is any number to the power of 0?
A: Any non-zero number raised to the power of 0 equals 1. For example, 5<sup>0</sup> = 1, and (-3)<sup>0</sup> = 1. The case of 0<sup>0</sup> is generally undefined.
Q: How do you calculate fractional exponents?
A: A fractional exponent represents a root. For example, a<sup>m/n</sup> = <sup>n</sup>√a<sup>m</sup>. So, 4<sup>1/2</sup> is the square root of 4, which is 2.
Q: Can exponents be decimals?
A: Yes, exponents can be decimals. Decimal exponents involve a combination of integer and fractional exponentiation principles. These are frequently encountered in scientific and engineering applications.
Q: What's the difference between exponents and multiplication?
A: Multiplication is repeated addition, while exponentiation is repeated multiplication. For example, 3 x 4 means adding 3 to itself four times (3+3+3+3), while 3<sup>4</sup> means multiplying 3 by itself four times (3x3x3x3).
Conclusion
In summary, understanding what 4 to the power of 3 means – that it equals 64, calculated as 4 x 4 x 4 – is a fundamental building block in mathematics. It opens the door to understanding more complex concepts, from algebraic equations to scientific notation and beyond. By mastering the basic rules of exponents and practicing regularly, you can unlock a powerful tool for problem-solving and critical thinking.
Now that you have a solid understanding of exponents, take the next step! Try applying your knowledge to real-world problems, explore more advanced topics like exponential functions, and challenge yourself with complex calculations. Share this article with your friends or classmates who are also learning about exponents, and discuss the concepts together. Your journey to mastering mathematics has just begun!
Latest Posts
Latest Posts
-
Frankenstein Junji Ito How Many Pages
Nov 22, 2025
-
The Great Gatsby Chapter One Summary
Nov 22, 2025
-
Is George Wilson A Static Or Dynamic Character
Nov 22, 2025
-
What Is 4 To The Power Of 3
Nov 22, 2025
-
How Many Obtuse Angles Are In An Obtuse Triangle
Nov 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.