What Is A 17 Out Of 25
sandbardeewhy
Nov 25, 2025 · 11 min read
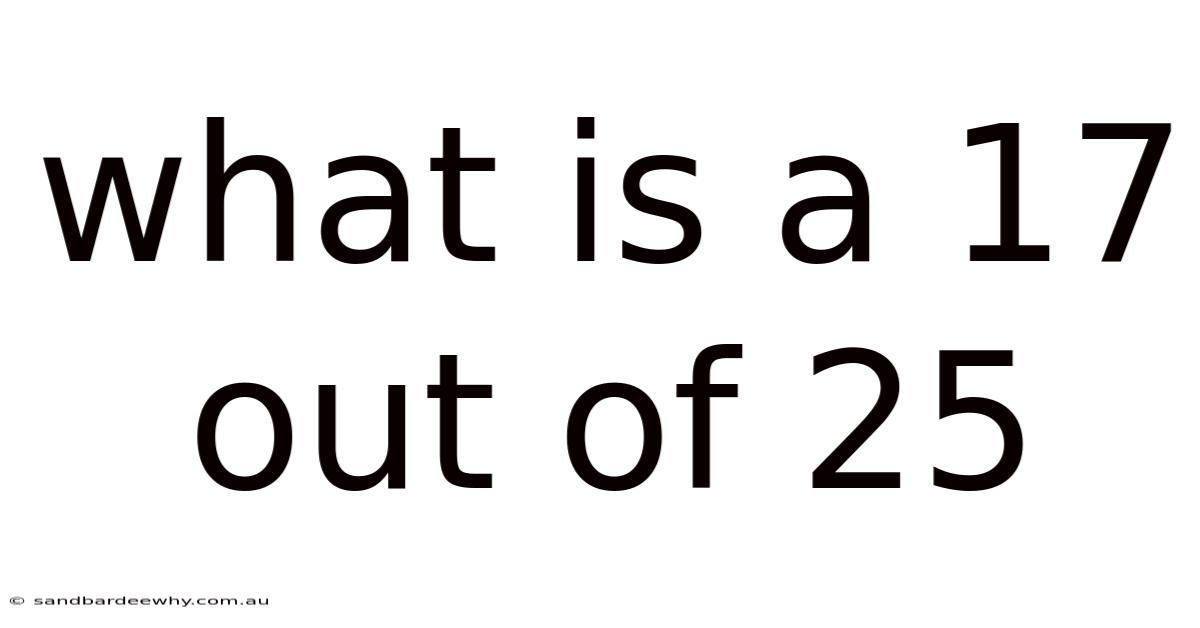
Table of Contents
Imagine receiving a test back and seeing "17/25" scrawled across the top. What does that number really mean? Is it a good score? A bad one? It’s easy to feel a pang of uncertainty when faced with a fraction that isn't immediately clear. Understanding how to interpret and work with fractions like 17/25 is a fundamental skill that extends far beyond the classroom. From calculating discounts while shopping to understanding proportions in recipes, fractions play a crucial role in everyday life.
At its core, a fraction like 17/25 simply represents a part of a whole. In this specific instance, the fraction seventeen twenty-fifths signifies that out of a total of 25 equal parts, we are considering 17 of those parts. It's a ratio, a comparison, and a key to unlocking a deeper understanding of numerical relationships. But what does 17/25 really tell us about performance, value, or quantity? This article will delve into the meaning of the fraction 17/25, explore its various representations, and provide practical ways to interpret and apply this knowledge across different contexts. From percentages and decimals to real-world scenarios, we'll equip you with the tools to confidently understand and utilize fractions in any situation.
Main Subheading
The fraction 17/25 is more than just two numbers separated by a line. It embodies a relationship, a proportion, and a specific quantity relative to a whole. To truly grasp its meaning, it’s helpful to break down its components and understand how it relates to other forms of numerical representation. The fraction 17/25 is a specific instance of a broader category of numbers that play a crucial role in mathematics and everyday life.
At its most basic, 17/25 is a fraction, a way to represent a part of a whole. The number above the line, 17, is called the numerator. It tells us how many parts we have. The number below the line, 25, is the denominator. It tells us the total number of equal parts that make up the whole. Think of a pizza cut into 25 equal slices; 17/25 represents 17 of those slices. Understanding this fundamental concept is the first step in unlocking the power of fractions.
Comprehensive Overview
Understanding the fraction 17/25 involves recognizing its different forms and the mathematical principles that govern it. This requires looking at fractions in a broader context and understanding their relationship with decimals, percentages, and ratios. To comprehensively understand this fraction, we need to consider its definition, scientific foundations, and historical context.
Definitions and Foundations: A fraction represents a part of a whole, as we've established. The fraction 17/25 is a rational number, meaning it can be expressed as a ratio of two integers (whole numbers). It's important to differentiate it from irrational numbers, like pi, which cannot be expressed as a simple fraction. The line separating the numerator and denominator signifies division. Therefore, 17/25 is mathematically equivalent to 17 divided by 25. This simple division is the key to converting the fraction into its decimal form.
Decimal Representation: To convert 17/25 to a decimal, you simply perform the division: 17 ÷ 25 = 0.68. A decimal is another way of representing a part of a whole, but instead of expressing it as a ratio, it uses a base-10 system. The decimal 0.68 signifies 68 hundredths. This means that 17/25 is equivalent to 68 out of 100. Understanding this equivalence is crucial for grasping the concept of percentages.
Percentage Representation: A percentage is a way of expressing a number as a fraction of 100. To convert a fraction to a percentage, you multiply the decimal form by 100. In this case, 0.68 * 100 = 68%. Therefore, 17/25 is equal to 68%. Percentages are widely used because they provide an easily understandable way to compare proportions. Seeing 68% immediately gives a sense of relative size compared to other percentages. For example, it is higher than 50%, which represents half of the total, and lower than 75%, which represents three-quarters.
Simplifying Fractions (When Possible): While 17/25 is already in its simplest form (because 17 is a prime number and doesn't share any factors with 25 other than 1), it's important to understand the concept of simplifying fractions. Simplifying involves dividing both the numerator and denominator by their greatest common factor (GCF). This reduces the fraction to its lowest terms without changing its value. For instance, the fraction 4/10 can be simplified to 2/5 by dividing both the numerator and denominator by 2. While not applicable to 17/25, this is a vital skill for working with other fractions.
Historical Context: The use of fractions dates back to ancient civilizations, with evidence found in Egyptian and Mesopotamian texts. Egyptians primarily used unit fractions (fractions with a numerator of 1), while Mesopotamians used sexagesimal fractions (fractions with a denominator of 60). The modern notation of fractions, with a horizontal line separating the numerator and denominator, developed gradually over centuries. Understanding the historical development of fractions provides a broader appreciation for their significance and the evolution of mathematical thought.
Trends and Latest Developments
While the fundamental principles of fractions remain constant, their application and interpretation continue to evolve with modern trends and data analysis. Understanding how fractions are used in contemporary contexts is essential for navigating an increasingly data-driven world. Current trends often involve using fractions and percentages to represent proportions in statistics, data visualization, and financial analysis.
Data Interpretation: In data analysis, fractions and percentages are frequently used to represent proportions and distributions. For example, a survey might reveal that 17 out of 25 respondents prefer a particular product. This can be expressed as the fraction 17/25 or, more commonly, as 68%. This allows for easy comparison with other data points. Imagine another survey shows that 75% of a different group prefers a competing product. The direct comparison between 68% and 75% provides immediate insight into the relative preferences of the two groups.
Financial Analysis: Fractions and percentages are ubiquitous in financial analysis. Interest rates, profit margins, and investment returns are often expressed as percentages. Understanding these percentages is crucial for making informed financial decisions. For example, if an investment promises a return of 8% annually, it means you'll earn 8/100 (or 0.08) of your initial investment each year.
Statistical Reporting: Statistical reports often rely on fractions and percentages to convey complex information in an accessible format. For instance, a report on unemployment rates might state that 5.2% of the workforce is unemployed. This percentage represents the fraction of the total workforce that is currently without a job.
Popular Opinion and Misinterpretations: It's also important to be aware of potential misinterpretations of fractions and percentages in popular opinion. For example, a headline might claim that "a third of the population supports a certain policy." While this sounds significant, it's crucial to consider the sample size and the margin of error. A third could represent a wide range of actual values, and it's important not to overstate the certainty of the claim.
Professional Insights: From a professional standpoint, understanding fractions and percentages is not just about calculation; it's about critical thinking and data literacy. Being able to interpret and analyze data presented in fractional or percentage form is essential for making informed decisions in various fields, from business and finance to science and healthcare. Professionals need to be able to quickly assess the significance of a percentage change, understand the implications of a fractional share, and identify potential biases or misrepresentations in data.
Tips and Expert Advice
Understanding fractions goes beyond theoretical knowledge. Applying practical tips and expert advice can significantly enhance your ability to work with fractions effectively in real-world scenarios. These tips focus on building a strong foundation, applying mental math techniques, and avoiding common mistakes.
Build a Strong Foundation: The key to mastering fractions is to build a solid understanding of the fundamental concepts. This includes understanding the meaning of the numerator and denominator, the relationship between fractions, decimals, and percentages, and the rules for performing basic operations like addition, subtraction, multiplication, and division. Take the time to review these basics if you feel unsure. Practice with visual aids, like fraction bars or pie charts, to solidify your understanding.
Master Mental Math Techniques: Developing mental math skills can significantly speed up your ability to work with fractions. For example, knowing common fraction-decimal-percentage equivalencies (like 1/4 = 0.25 = 25%) can save you time and effort. Practice estimating fractions and percentages in your head. For instance, if you need to calculate 65% of $80, you can estimate that 65% is a little more than 60%, which is close to 2/3. Since 2/3 of $80 is roughly $53, you know that 65% of $80 will be somewhere around that amount.
Convert to Percentages for Easier Comparison: When comparing different fractions, converting them to percentages can make the comparison much easier. Percentages provide a common scale that allows you to quickly assess the relative size of different fractions. For example, comparing 3/8 and 17/25 directly can be challenging. However, converting them to percentages (37.5% and 68%, respectively) makes it immediately clear that 17/25 is significantly larger.
Use Real-World Examples: Applying fractions to real-world scenarios can help solidify your understanding and make them more relevant. For example, when cooking, you might need to double a recipe that calls for 2/3 cup of flour. Understanding how to multiply fractions will allow you to accurately adjust the recipe. Similarly, when shopping, you might encounter discounts expressed as percentages. Knowing how to calculate percentages will help you determine the actual sale price.
Avoid Common Mistakes: One common mistake is to add or subtract fractions without finding a common denominator. Another is to confuse fractions and ratios. Remember that a fraction represents a part of a whole, while a ratio compares two separate quantities. Be mindful of these common pitfalls and double-check your work to avoid errors.
Seek Out Resources and Practice: There are countless resources available to help you improve your understanding of fractions. Online tutorials, practice worksheets, and educational videos can provide valuable support. Don't be afraid to ask for help from teachers, tutors, or friends. The key is to practice regularly and to approach fractions with a positive and inquisitive attitude.
FAQ
Q: What does 17/25 mean in simple terms?
A: It means 17 out of 25 equal parts of something. Think of it as having 17 slices of a pizza that was originally cut into 25 slices.
Q: How do I convert 17/25 to a percentage?
A: Divide 17 by 25 to get 0.68, then multiply by 100 to get 68%. So, 17/25 is equal to 68%.
Q: Is 17/25 a good grade?
A: That depends on the context and grading scale. However, 68% is generally considered a passing grade, often equivalent to a C or D.
Q: Can 17/25 be simplified?
A: No, 17/25 is already in its simplest form. The numbers 17 and 25 do not share any common factors other than 1.
Q: How is 17/25 used in real life?
A: It can be used to represent proportions, ratios, or probabilities. For example, if 17 out of 25 people in a survey prefer a certain product, that preference can be expressed as 17/25 or 68%.
Conclusion
In summary, the fraction 17/25 represents a specific proportion, a part of a whole divided into 25 equal segments, with 17 of those segments being considered. This fraction can be expressed as a decimal (0.68) or a percentage (68%), providing different perspectives on the same underlying quantity. Understanding how to interpret and convert between these forms is crucial for applying fractions in various real-world contexts, from interpreting data and making financial decisions to understanding proportions in recipes.
By mastering the fundamentals of fractions and applying practical tips, you can confidently navigate situations involving fractional quantities and make informed decisions based on proportional reasoning. Don't stop here! Practice converting other fractions to decimals and percentages, explore different real-world applications, and continue to build your understanding of this essential mathematical concept. Share this article with friends or colleagues who might find it helpful, and leave a comment below with your own examples of how you use fractions in your daily life.
Latest Posts
Latest Posts
-
What Is 500 Ml In Oz
Nov 25, 2025
-
How Many Valence Electrons Does Hydrogen Have
Nov 25, 2025
-
What Is 17 Out Of 20 As A Percentage
Nov 25, 2025
-
Names Of The Families In Romeo And Juliet
Nov 25, 2025
-
How Do You Add Square Roots
Nov 25, 2025
Related Post
Thank you for visiting our website which covers about What Is A 17 Out Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.