What Is Half Of 3 1 3
sandbardeewhy
Nov 26, 2025 · 10 min read
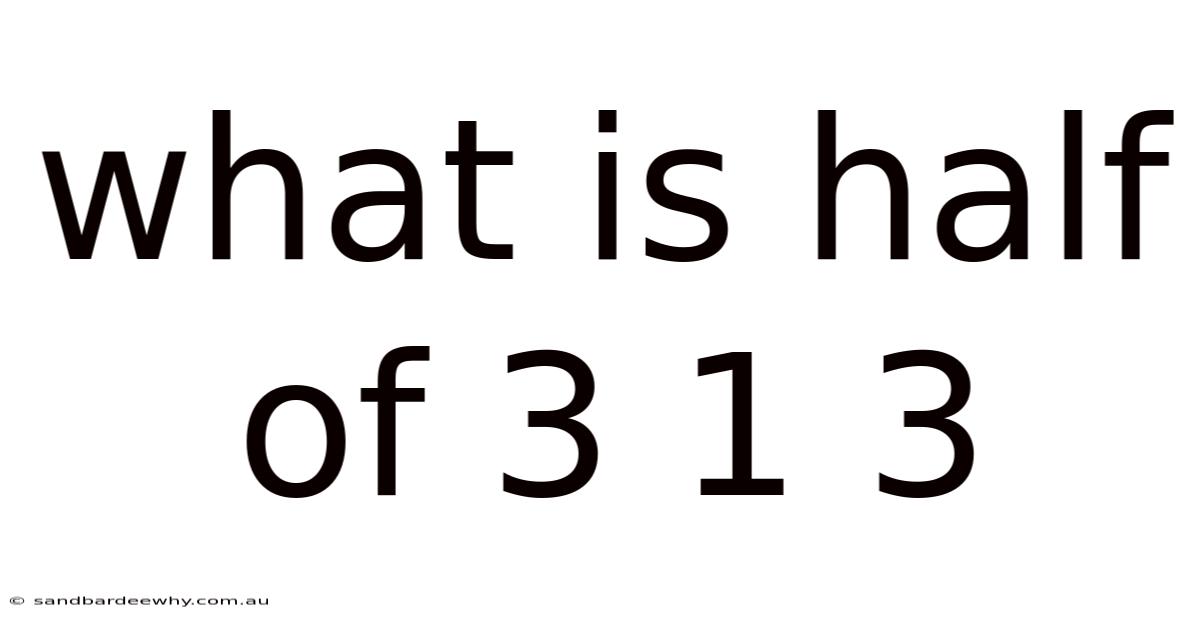
Table of Contents
Imagine you're at a bakery, eyeing a delicious three-layer cake. Someone asks, "What's half of three and one-third cakes?" You might instinctively think, "One and a half, plus a little extra from that third." But how do you get to the exact number, and more importantly, understand the math behind it?
This simple question, "What is half of 3 1/3," opens a door to a world of fractions, mixed numbers, and fundamental arithmetic. While seemingly straightforward, it requires a solid grasp of mathematical principles to arrive at the correct answer. This article will explore the question in detail, breaking down the steps and underlying concepts to ensure you not only understand the solution but also the reasoning behind it.
Understanding Half of 3 1/3
Before diving into the solution, let's clarify what we're trying to find. We want to calculate what you get when you divide the mixed number 3 1/3 by 2. This involves a few steps: first, converting the mixed number to an improper fraction, and then performing the division. Let's delve deeper into the mathematics that enables us to solve this.
At its core, finding half of a number means dividing that number by 2. This applies to whole numbers, fractions, and mixed numbers alike. The real challenge comes in handling the mixed number, which combines a whole number and a fraction. Understanding how to manipulate mixed numbers is essential not only for this specific problem but for a wide range of mathematical applications.
The journey to answering "What is half of 3 1/3" showcases the elegance and practicality of basic arithmetic. By breaking down the problem into smaller, manageable steps, we can conquer what might initially seem like a complex question. So, let's embark on this mathematical exploration together and uncover the solution.
Comprehensive Overview of Fractions and Mixed Numbers
To accurately determine half of 3 1/3, we must first have a firm understanding of fractions and mixed numbers. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). For example, in the fraction 1/2, 1 is the numerator and 2 is the denominator, indicating one part out of two equal parts.
A mixed number, on the other hand, combines a whole number and a fraction. The number 3 1/3 is a mixed number, where 3 is the whole number and 1/3 is the fractional part. Mixed numbers are a convenient way to represent quantities greater than one when a fraction is also involved. Understanding how to convert between mixed numbers and improper fractions is crucial for performing arithmetic operations.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator, such as 5/3. Converting a mixed number to an improper fraction is a fundamental step in many calculations. To convert 3 1/3 to an improper fraction, you multiply the whole number (3) by the denominator (3) and add the numerator (1), then place the result over the original denominator. So, (3 * 3) + 1 = 10, making the improper fraction 10/3.
The concept of fractions has ancient roots, with evidence of their use dating back to ancient Egypt and Mesopotamia. Egyptians used fractions extensively in their calculations for land division, construction, and accounting. They primarily worked with unit fractions (fractions with a numerator of 1). The Babylonians, on the other hand, developed a sophisticated number system based on 60, which allowed them to represent fractions more accurately.
Understanding fractions and mixed numbers is not just an academic exercise; it has practical applications in everyday life. Whether you're doubling a recipe, splitting a bill, or measuring ingredients, fractions are indispensable. Mastering these concepts builds a strong foundation for more advanced mathematical topics and enhances problem-solving skills in various fields.
Trends and Latest Developments in Math Education
In math education, there is a growing emphasis on conceptual understanding rather than rote memorization. Educators are increasingly using visual aids, hands-on activities, and real-world examples to help students grasp the underlying principles of fractions and mixed numbers. This approach aims to make math more engaging and relevant, fostering a deeper understanding that students can apply in various contexts.
One popular trend is the use of technology in math education. Interactive simulations, educational apps, and online resources provide students with opportunities to explore fractions and mixed numbers in a dynamic and interactive way. These tools can help visualize abstract concepts, provide immediate feedback, and cater to different learning styles.
Another trend is the focus on problem-solving and critical thinking skills. Instead of simply memorizing formulas, students are encouraged to analyze problems, develop strategies, and explain their reasoning. This approach promotes a deeper understanding of mathematical concepts and prepares students for real-world challenges. For example, word problems that involve fractions and mixed numbers can help students see the practical applications of these concepts.
Professional insights suggest that a strong foundation in fractions is crucial for success in higher-level math courses. Students who struggle with fractions often face difficulties in algebra, calculus, and other advanced topics. Therefore, educators are focusing on early intervention and providing targeted support to students who need extra help with fractions. This includes individualized instruction, small group work, and peer tutoring.
The shift towards conceptual understanding and problem-solving skills reflects a broader trend in education towards preparing students for the demands of the 21st century. Employers are increasingly looking for individuals who can think critically, solve complex problems, and communicate effectively. A solid foundation in math, particularly in areas like fractions and mixed numbers, is essential for developing these skills.
Tips and Expert Advice for Working with Fractions
Working with fractions can sometimes be challenging, but with the right strategies, it can become much easier. Here are some tips and expert advice to help you master fractions and mixed numbers:
-
Always simplify fractions: Before performing any operations, simplify the fractions involved. Simplifying means reducing the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common factor (GCF). For example, the fraction 4/6 can be simplified to 2/3 by dividing both 4 and 6 by 2. Simplifying fractions makes calculations easier and reduces the chances of making errors.
-
Convert mixed numbers to improper fractions: When performing operations like multiplication or division with mixed numbers, it's often easier to convert them to improper fractions first. As mentioned earlier, to convert a mixed number to an improper fraction, multiply the whole number by the denominator and add the numerator, then place the result over the original denominator. This step ensures that you're working with a single fraction, which simplifies the calculations.
-
Find a common denominator: When adding or subtracting fractions, you need to have a common denominator. This means that the denominators of all the fractions must be the same. To find a common denominator, you can find the least common multiple (LCM) of the denominators. Once you have a common denominator, you can add or subtract the numerators while keeping the denominator the same.
-
Use visual aids: Visual aids can be incredibly helpful for understanding fractions. Diagrams, fraction bars, and pie charts can help you visualize the concept of fractions and make it easier to understand how they relate to each other. For example, you can use a pie chart to show that 1/2 + 1/2 = 1.
-
Practice regularly: Like any skill, working with fractions requires practice. The more you practice, the more comfortable you'll become with the concepts and the easier it will be to solve problems. Try working through a variety of problems, from simple to complex, to challenge yourself and reinforce your understanding.
-
Estimate your answers: Before solving a problem involving fractions, try to estimate the answer. This can help you check your work and make sure your answer is reasonable. For example, if you're trying to find half of 3 1/3, you know that the answer should be somewhere around 1 1/2. If your calculated answer is significantly different from your estimate, you know that you've made a mistake.
By following these tips and practicing regularly, you can improve your understanding of fractions and mixed numbers and become more confident in your ability to work with them.
FAQ: Frequently Asked Questions
Q: What is a mixed number?
A: A mixed number is a combination of a whole number and a fraction. For example, 3 1/3 is a mixed number where 3 is the whole number and 1/3 is the fraction.
Q: How do you convert a mixed number to an improper fraction?
A: To convert a mixed number to an improper fraction, multiply the whole number by the denominator of the fraction, add the numerator, and then place the result over the original denominator. For example, to convert 3 1/3 to an improper fraction, you would calculate (3 * 3) + 1 = 10, so the improper fraction is 10/3.
Q: Why do you need a common denominator when adding or subtracting fractions?
A: You need a common denominator when adding or subtracting fractions because you can only add or subtract fractions that have the same size parts. The denominator tells you how many equal parts the whole is divided into, so you need the denominators to be the same to ensure you're adding or subtracting parts of the same size.
Q: What is the greatest common factor (GCF)?
A: The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of them. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides evenly into both 12 and 18.
Q: What is the least common multiple (LCM)?
A: The least common multiple (LCM) of two or more numbers is the smallest number that is a multiple of all of them. For example, the LCM of 4 and 6 is 12 because 12 is the smallest number that is a multiple of both 4 and 6.
Q: How can visual aids help with understanding fractions?
A: Visual aids like diagrams, fraction bars, and pie charts can help you visualize the concept of fractions and make it easier to understand how they relate to each other. They provide a concrete representation of fractions, making it easier to grasp the underlying principles.
Conclusion
In summary, finding half of 3 1/3 involves converting the mixed number to an improper fraction (10/3), and then dividing that fraction by 2, which results in 5/3. This can then be converted back to a mixed number, giving us 1 2/3. Thus, half of 3 1/3 is 1 2/3.
Mastering these basic mathematical concepts, such as working with fractions and mixed numbers, is not just about solving equations; it's about developing a way of thinking that can be applied to countless real-world situations. A solid understanding of fractions is a foundational skill that empowers you to tackle more complex mathematical problems and make informed decisions in your daily life.
Now that you've explored the ins and outs of finding half of 3 1/3, why not put your new knowledge to the test? Try solving similar problems with different mixed numbers. Share your solutions or any remaining questions in the comments below. Let's continue the learning journey together!
Latest Posts
Latest Posts
-
Romeo And Juliet First Act Summary
Nov 26, 2025
-
What Are The Features Of A Text
Nov 26, 2025
-
How Many Ounces In A Quart Of Water
Nov 26, 2025
-
What Is Half Of 3 1 3
Nov 26, 2025
-
How Many Pounds Are In 2 Tons
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 3 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.