What Percent Is 15 Of 25
sandbardeewhy
Nov 23, 2025 · 13 min read
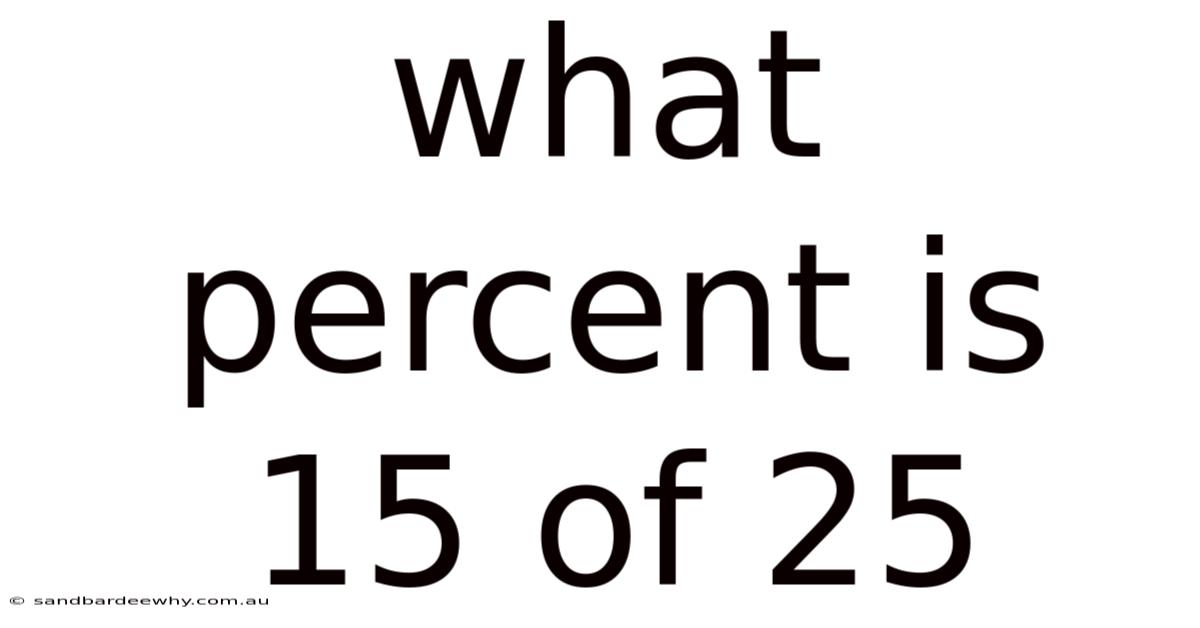
Table of Contents
Have you ever found yourself in a situation where you needed to quickly calculate a percentage but didn't have a calculator handy? Maybe you were splitting a bill with friends and wanted to figure out the tip, or perhaps you were trying to determine the discount on an item at your favorite store. Understanding how to calculate percentages is a fundamental skill that can be incredibly useful in everyday life.
In this article, we will explore the simple yet powerful concept of calculating percentages, focusing specifically on how to determine what percent 15 is of 25. By the end of this guide, you’ll not only know the answer but also understand the underlying principles and methods that allow you to solve similar problems with confidence. Whether you're a student brushing up on your math skills, a professional seeking to sharpen your analytical abilities, or just someone looking to enhance your everyday math skills, this comprehensive guide will provide you with the knowledge and tools you need.
Main Subheading
Percentages are a fundamental concept in mathematics with applications that span across various fields, from finance and statistics to everyday shopping and cooking. Understanding what percentages are, how they are derived, and how to calculate them is crucial for making informed decisions and solving practical problems. A percentage is essentially a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." This concept provides a standardized way to compare different quantities and understand their relative sizes.
At its core, a percentage represents a ratio or fraction where the denominator is always 100. For example, 50% means 50 out of 100, which can also be written as the fraction 50/100 or the decimal 0.50. This standardization allows for easy comparison; if you know that one quantity is 25% of a whole and another is 75% of the same whole, you immediately understand their relative proportions. Percentages are particularly useful because they convert various fractions and ratios into a common scale, making it easier to interpret and communicate numerical information.
Comprehensive Overview
Defining Percentages and Their Importance
A percentage is a dimensionless number, meaning it doesn't have any units. It's simply a way to express a part of a whole as a fraction of 100. The symbol "%" is used to denote percentages, making it easy to identify and interpret them in various contexts. Understanding percentages is vital because they offer a standardized way to express proportions, enabling comparisons across different scales and contexts.
Percentages are extensively used in various fields:
- Finance: Interest rates, investment returns, and profit margins are often expressed as percentages. Understanding these values helps in making sound financial decisions.
- Statistics: Percentages are used to present data in a clear and understandable format, such as in surveys, polls, and demographic analyses.
- Retail: Discounts, sales tax, and markups are commonly expressed as percentages, influencing consumer purchasing decisions.
- Health: Body fat percentage, success rates of medical treatments, and nutritional information are often conveyed using percentages.
The Mathematical Foundation of Percentages
The foundation of percentages lies in basic arithmetic operations, particularly division and multiplication. To calculate what percent one number is of another, you typically use the following formula:
Percentage = (Part / Whole) * 100
Here, "Part" refers to the value you want to express as a percentage of the "Whole," which is the total or reference value. By dividing the part by the whole and then multiplying by 100, you convert the ratio into a percentage.
For example, if you want to find what percent 15 is of 25, you would perform the calculation as follows:
Percentage = (15 / 25) * 100
This formula provides a direct and straightforward method for converting any ratio into a percentage, making it an essential tool in quantitative analysis.
Historical Context of Percentages
The concept of percentages has ancient roots, dating back to the Roman Empire. The Romans used a system similar to percentages when levying taxes. Emperor Augustus, for example, imposed a tax of centesima rerum venalium, which was 1/100 of the value of goods sold at auction. This was essentially a 1% tax.
The use of percentages became more widespread during the Middle Ages, particularly in commercial activities. As trade and banking developed, merchants and financiers needed a standardized way to calculate interest, profit, and loss. The adoption of the decimal system in Europe further facilitated the use of percentages, making calculations easier and more accessible. By the 15th century, percentages were a standard tool in mathematical texts and commercial practices, solidifying their place in the world of finance and trade.
Methods to Calculate Percentages
There are several methods to calculate percentages, each suited to different scenarios and preferences. Understanding these methods can provide flexibility and efficiency in problem-solving.
- Formula Method: This is the most straightforward method, using the formula
Percentage = (Part / Whole) * 100. It is applicable in a wide range of situations and is particularly useful when precision is required. - Fraction Method: Convert the part and whole into a fraction and simplify it. Then, convert the simplified fraction into a percentage. For example, if you want to find what percent 15 is of 25, you can write it as 15/25, which simplifies to 3/5. To convert 3/5 to a percentage, multiply by 100: (3/5) * 100 = 60%.
- Decimal Method: Divide the part by the whole to get a decimal, and then multiply the decimal by 100 to convert it into a percentage. For instance, if you want to find what percent 8 is of 20, divide 8 by 20 to get 0.4. Then, multiply 0.4 by 100 to get 40%.
- Proportion Method: Set up a proportion to find the percentage. A proportion is an equation stating that two ratios are equal. For example, if you want to find what percent 12 is of 40, you can set up the proportion:
12/40 = x/100. Cross-multiply to solve for x:40x = 1200, sox = 30. Therefore, 12 is 30% of 40.
Common Mistakes in Percentage Calculations
While calculating percentages is generally straightforward, several common mistakes can lead to incorrect results. Being aware of these pitfalls can help you avoid errors and ensure accuracy.
- Misidentifying the Part and Whole: One of the most frequent errors is confusing the part and the whole in the calculation. Always ensure that you are dividing the correct value by the appropriate reference value. For example, if the question is "What percent of 50 is 20?", make sure you divide 20 by 50, not the other way around.
- Forgetting to Multiply by 100: After dividing the part by the whole, it is essential to multiply the result by 100 to convert it into a percentage. Failing to do so will give you a decimal value, not a percentage.
- Incorrectly Applying Percentage Increase or Decrease: When calculating percentage increases or decreases, it's crucial to use the original value as the reference point. For instance, if a price increases from $20 to $25, the percentage increase is calculated as
((25 - 20) / 20) * 100 = 25%. - Rounding Errors: Rounding numbers prematurely can lead to inaccuracies in the final percentage. It's generally best to perform the calculations with as much precision as possible and round the final result to the desired level of accuracy.
Trends and Latest Developments
Current Applications of Percentages
In today's data-driven world, percentages continue to be a vital tool for analysis and communication. Here are some areas where percentages are particularly relevant:
- Market Research: Companies use percentages to analyze market share, customer satisfaction, and sales trends. These insights help in making strategic decisions about product development, marketing, and sales strategies.
- Economics: Economic indicators such as inflation rates, unemployment rates, and GDP growth are often expressed as percentages. These figures provide a snapshot of the economy's health and performance.
- Social Sciences: Researchers use percentages to analyze survey data, demographic trends, and social behaviors. This information helps in understanding societal changes and informing public policy.
- Technology: Percentages are used in computer science to measure algorithm efficiency, data compression rates, and network performance. They are also used in machine learning to evaluate model accuracy and precision.
Recent Data and Statistics Involving Percentages
Recent data and statistics highlight the ongoing importance of percentages in various fields:
- E-commerce Growth: The percentage of retail sales occurring online has been steadily increasing. According to recent reports, e-commerce sales now account for a significant percentage of total retail sales worldwide, reflecting the shift towards online shopping.
- Healthcare Statistics: The percentage of the population vaccinated against various diseases is a critical metric in public health. Monitoring vaccination rates helps in preventing outbreaks and protecting vulnerable populations.
- Environmental Data: The percentage of renewable energy sources in the energy mix is a key indicator of sustainability efforts. Many countries are setting targets to increase the percentage of renewable energy in their energy production.
- Financial Markets: Interest rates and investment returns are constantly tracked and analyzed using percentages. These figures influence investment decisions and overall market stability.
Expert Insights on Percentage Usage
Experts emphasize the importance of understanding the context and limitations of percentage data:
- Context Matters: Percentages should always be interpreted in context. A high percentage may not always indicate a large absolute value, and vice versa. Understanding the base value is crucial for accurate interpretation.
- Beware of Misleading Visualizations: Visual representations of percentage data, such as charts and graphs, can sometimes be misleading. It's important to critically evaluate these visualizations and ensure they accurately reflect the underlying data.
- Consider Sample Size: When analyzing percentages derived from sample data, it's important to consider the sample size. Small sample sizes can lead to unreliable percentages that may not accurately represent the population.
- Use Percentages in Conjunction with Other Metrics: Percentages should be used in conjunction with other relevant metrics to provide a comprehensive understanding of the situation. Relying solely on percentages can lead to oversimplification and inaccurate conclusions.
Tips and Expert Advice
Practical Tips for Accurate Percentage Calculations
Calculating percentages accurately is a fundamental skill, but it requires attention to detail. Here are some practical tips to ensure your calculations are precise and reliable:
- Double-Check Your Inputs: Always verify that you are using the correct values for the "Part" and the "Whole." Misidentifying these values is a common source of error.
- Use a Calculator or Spreadsheet: For complex calculations or when dealing with large numbers, use a calculator or spreadsheet software like Microsoft Excel or Google Sheets. These tools minimize the risk of manual calculation errors.
- Understand the Question: Make sure you fully understand what the question is asking. Are you calculating a percentage increase, a percentage decrease, or simply what percent one number is of another? The type of calculation will affect the formula you use.
Real-World Examples of Percentage Use
To further illustrate the practical application of percentages, let's consider some real-world examples:
- Calculating Sales Tax: When purchasing an item, you often need to calculate the sales tax. If an item costs $50 and the sales tax is 8%, you can calculate the tax amount as follows:
Tax = (8/100) * 50 = $4. The total cost of the item is then $50 + $4 = $54. - Determining Discounted Prices: Retailers often offer discounts expressed as percentages. If an item originally priced at $100 is on sale for 25% off, the discount amount is
Discount = (25/100) * 100 = $25. The sale price is then $100 - $25 = $75. - Analyzing Investment Returns: Investors often evaluate their returns as percentages. If you invest $1,000 and earn $50 in profit, your return on investment (ROI) is
ROI = (50/1000) * 100 = 5%.
Strategies for Simplifying Percentage Problems
Simplifying percentage problems can make them easier to solve, especially when you don't have a calculator available. Here are some strategies to help you:
- Convert Percentages to Fractions: Converting percentages to fractions can simplify calculations. For example, 25% is equivalent to 1/4, 50% is equivalent to 1/2, and 75% is equivalent to 3/4.
- Use Mental Math Tricks: Develop mental math skills to perform quick percentage calculations. For example, to find 10% of a number, simply move the decimal point one place to the left. To find 5% of a number, find 10% and then divide by 2.
- Break Down Complex Problems: Break down complex percentage problems into smaller, more manageable steps. For example, if you need to calculate a series of discounts or markups, perform each calculation separately.
By applying these tips and strategies, you can enhance your ability to calculate percentages accurately and efficiently in various real-world scenarios.
FAQ
Q: What is the formula for calculating a percentage?
A: The basic formula for calculating a percentage is: Percentage = (Part / Whole) * 100. This formula is used to find what percent one number (the "Part") is of another number (the "Whole").
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase or decrease, use the formula: Percentage Change = ((New Value - Original Value) / Original Value) * 100. If the result is positive, it's a percentage increase; if it's negative, it's a percentage decrease.
Q: What is the difference between a percentage and a percentile?
A: A percentage is a ratio or fraction expressed as a fraction of 100, while a percentile is a measure used in statistics indicating the value below which a given percentage of observations in a group of observations falls.
Q: How do I convert a fraction to a percentage?
A: To convert a fraction to a percentage, divide the numerator by the denominator and then multiply the result by 100. For example, to convert 3/4 to a percentage, calculate (3/4) * 100 = 75%.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100% in situations where the "Part" is larger than the "Whole." For example, if a company's sales increase by 150% compared to the previous year, the sales are now 2.5 times the original amount.
Conclusion
Understanding how to calculate percentages is a fundamental skill that is essential in various aspects of life, from finance and shopping to statistics and everyday problem-solving. In this article, we focused on answering the question: "What percent is 15 of 25?" By applying the formula Percentage = (Part / Whole) * 100, we find that 15 is 60% of 25.
Whether you're a student, a professional, or simply someone looking to improve your math skills, mastering the art of percentage calculations can empower you to make informed decisions and navigate the complexities of the modern world with confidence. Now that you have a solid grasp of the concepts and methods discussed in this guide, put your knowledge to the test. Try solving various percentage problems and exploring real-world applications to further enhance your understanding.
Don't stop here—continue to explore the world of mathematics and discover the endless possibilities it offers. Share this article with friends, family, or colleagues who might benefit from it, and let's continue learning and growing together.
Latest Posts
Latest Posts
-
How Many Pounds In 72 Kilos
Nov 23, 2025
-
5 Yards Is How Many Inches
Nov 23, 2025
-
How Many Gallons In 15 Litres
Nov 23, 2025
-
How Many Miles Per Hour Is 20 Knots
Nov 23, 2025
-
What Percentage Of 15 Is 12
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 15 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.