What Percent Is 19 Of 25
sandbardeewhy
Nov 28, 2025 · 12 min read
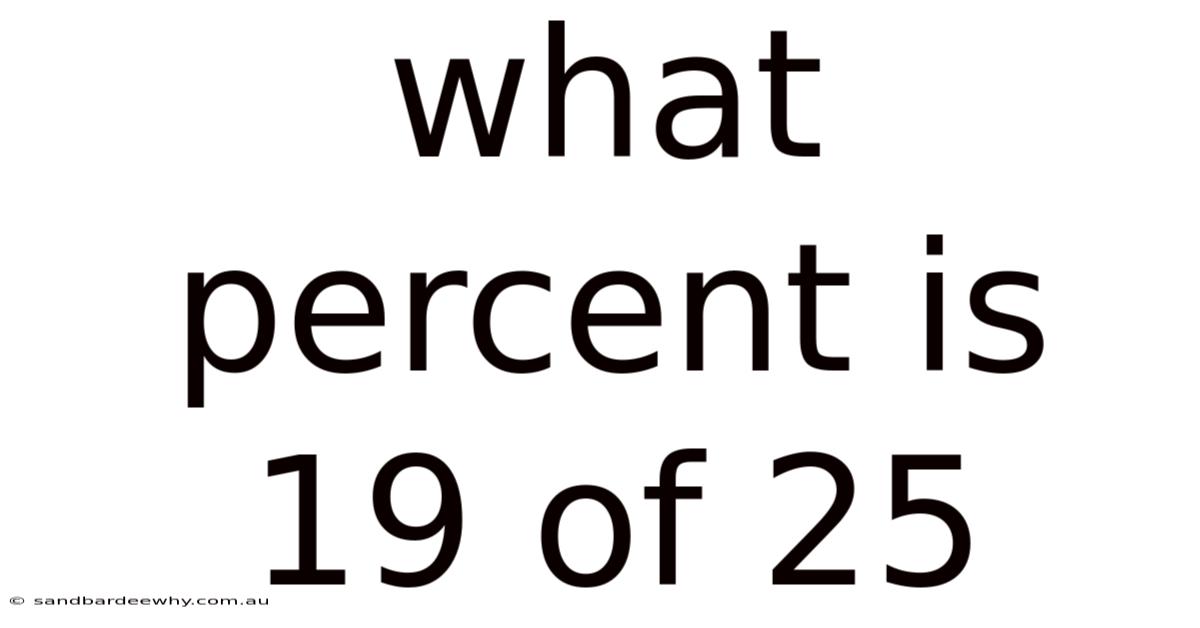
Table of Contents
Imagine you're at a bustling farmers market, eyeing a basket of plump, ripe strawberries. The sign reads "25 Strawberries - Special Today!" You decide you only want 19 of them. What portion of the whole basket are you taking? Figuring out what percent is 19 of 25 is the same as calculating your share of those delicious berries. It's a fundamental math skill with everyday applications.
Calculating percentages is more than just a classroom exercise; it's a practical tool for understanding proportions, discounts, statistics, and much more. Whether you're splitting a bill, calculating sales tax, or analyzing survey results, knowing how to find what percent one number is of another empowers you to make informed decisions. This article will delve into the simple yet powerful concept of percentage calculation, focusing on how to determine what percent 19 is of 25, while providing a comprehensive understanding that extends beyond this specific example.
Understanding the Basics of Percentage
At its core, a percentage is a way to express a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." Think of it as a standardized way to compare proportions, making it easy to grasp the relative size of different quantities. Understanding percentages is crucial in various fields, from finance and statistics to everyday shopping and cooking.
Percentages provide a universal scale for comparison. For instance, saying that 19 out of 25 students passed a test gives you some information, but expressing it as a percentage (76%) allows for immediate comparison with other classes or schools, regardless of the total number of students. This standardization is what makes percentages such a powerful tool for communication and analysis.
The Formula
The fundamental formula for calculating what percent one number is of another is remarkably simple:
Percentage = (Part / Whole) * 100
- Part: The specific quantity you're interested in (in our case, 19).
- Whole: The total or reference quantity (in our case, 25).
Applying this formula to our initial question, "What percent is 19 of 25?", we substitute the values:
Percentage = (19 / 25) * 100
The result of this calculation will give us the percentage that 19 represents out of the total of 25. This basic formula is the key to unlocking a wide range of percentage-related problems.
The Math Behind the Example
Let's break down the calculation step-by-step:
- Divide the Part by the Whole: Divide 19 by 25. 19 ÷ 25 = 0.76
- Multiply by 100: Multiply the result by 100 to convert the decimal into a percentage. 0.76 * 100 = 76
Therefore, 19 is 76% of 25. This straightforward calculation demonstrates the power and simplicity of the percentage formula. It showcases how a simple division followed by multiplication can reveal the proportional relationship between two numbers.
Why This Matters
Understanding how to calculate percentages isn't just about solving math problems; it's about developing critical thinking and analytical skills that are invaluable in everyday life. From understanding discounts at the store to interpreting statistical data in news articles, the ability to work with percentages empowers you to make informed decisions.
Consider a scenario where you're comparing two investment options. One option boasts a 5% annual return on a $10,000 investment, while the other offers a 7% return on a $5,000 investment. While the latter has a higher percentage return, understanding how to calculate the actual dollar amount of the return will help you determine which investment is actually more profitable. Percentages provide a standardized way to compare these returns, but it's the ability to translate those percentages into real-world values that makes the difference.
Connecting to Proportions and Ratios
Percentages are closely related to proportions and ratios. A ratio expresses the relative size of two or more values, while a proportion states that two ratios are equal. Percentages can be seen as a special type of ratio where the second term is always 100.
For example, the ratio of 19 to 25 can be written as 19:25. This ratio represents the same relationship as the percentage 76%. Understanding this connection allows you to translate between ratios, proportions, and percentages seamlessly.
Trends and Latest Developments in Percentage Use
While the core concept of percentage calculation remains constant, its application evolves with changing trends and technological advancements. In recent years, we've seen an increased emphasis on data analysis and visualization, which has further amplified the importance of understanding percentages.
One prominent trend is the use of interactive dashboards and data visualization tools in business and finance. These tools rely heavily on percentages to present complex data in an easily digestible format. For instance, a marketing dashboard might display the percentage increase in website traffic, the percentage of leads converted into customers, or the percentage of customer satisfaction. These visualizations allow decision-makers to quickly identify trends and make informed choices.
The Role of Technology
Technology has also played a significant role in simplifying percentage calculations. Online calculators, spreadsheet software, and mobile apps make it easier than ever to perform complex calculations quickly and accurately. However, it's crucial to understand the underlying principles behind these tools, rather than simply relying on them blindly. A strong conceptual understanding of percentages allows you to critically evaluate the results generated by these tools and identify potential errors.
Furthermore, the rise of big data has created a need for more sophisticated percentage-based analysis. Statisticians and data scientists use percentages to analyze large datasets, identify patterns, and make predictions. For example, in healthcare, percentages are used to track the prevalence of diseases, measure the effectiveness of treatments, and monitor patient outcomes. In finance, percentages are used to analyze market trends, assess investment risks, and manage portfolios.
Public Opinion and Statistical Literacy
Another important trend is the growing awareness of the importance of statistical literacy. In an age of information overload, it's crucial to be able to critically evaluate data presented in the media, in political discourse, and in everyday conversations. Understanding percentages is a key component of statistical literacy, as it allows you to interpret data accurately and identify potential biases or misrepresentations.
For instance, consider a news headline that claims "Unemployment Rate Drops to 5%." While this might seem like good news, it's important to understand what this percentage actually represents. What population is being measured? What methodology is being used to collect the data? Understanding the nuances of percentage-based statistics allows you to form your own informed opinions, rather than simply accepting information at face value.
Ethical Considerations
Finally, it's important to consider the ethical implications of using percentages. Percentages can be powerful tools for persuasion, and they can be easily manipulated to present a biased or misleading picture. For example, a company might claim a "50% Increase in Sales!" without mentioning that the sales were previously very low. Being aware of these potential pitfalls is crucial for both consumers and professionals who work with data.
In summary, while the basic formula for calculating percentages remains the same, the way we use and interpret percentages is constantly evolving. From data visualization and statistical analysis to ethical considerations and public opinion, understanding percentages is more important than ever in today's world.
Practical Tips and Expert Advice for Mastering Percentages
Now that we've covered the fundamentals and current trends, let's delve into some practical tips and expert advice to help you master the art of percentage calculation and application.
1. Develop a Strong Number Sense: A solid foundation in basic arithmetic is essential for working with percentages. Practice your multiplication, division, addition, and subtraction skills to improve your speed and accuracy. The more comfortable you are with these fundamental operations, the easier it will be to work with percentages.
- Real-World Example: When calculating a 15% tip on a restaurant bill, quickly estimate 10% of the bill and then add half of that amount to get the tip amount.
2. Practice Converting Between Percentages, Decimals, and Fractions: Percentages, decimals, and fractions are all different ways of representing the same proportion. Being able to convert seamlessly between these forms is crucial for solving percentage problems. Remember that a percentage is simply a decimal multiplied by 100, and a fraction can be converted to a decimal by dividing the numerator by the denominator.
- Real-World Example: If a store offers a "1/4 Off" sale, recognize that this is equivalent to 0.25 and 25%.
3. Use Benchmarks and Estimations: When dealing with complex percentage problems, use benchmarks and estimations to check your answers and ensure they are reasonable. For example, if you're calculating a discount of 22% on an item, you can estimate by rounding to 20% and calculating that amount. This will give you a rough idea of what the final answer should be.
- Real-World Example: Before calculating the exact percentage discount on a large purchase, estimate the potential savings to determine if the sale is truly worthwhile.
4. Understand Different Types of Percentage Problems: Be aware of the different types of percentage problems you might encounter. Some common types include:
* **Finding a Percentage of a Number:** (e.g., What is 20% of 50?)
* **Finding What Percentage One Number Is of Another:** (e.g., What percent is 19 of 25?)
* **Finding the Whole When Given a Percentage:** (e.g., 10 is 25% of what number?)
* **Percentage Increase/Decrease:** (e.g., What is the percentage increase from 20 to 30?)
- Expert Advice: Practice identifying the type of problem you're facing before attempting to solve it. This will help you choose the correct formula and avoid common errors.
5. Leverage Technology Wisely: While online calculators and software can be helpful, don't rely on them blindly. Use them as tools to check your work and speed up calculations, but always understand the underlying principles.
- Caution: Be wary of online calculators that don't clearly explain their methodology or that produce results that seem unreasonable.
6. Apply Percentages to Real-World Scenarios: The best way to master percentages is to apply them to real-world scenarios. Look for opportunities to use percentages in your everyday life, whether it's calculating discounts, splitting bills, or analyzing statistics.
- Activity: Track your expenses for a month and calculate the percentage of your income that you spend on different categories, such as housing, food, and entertainment.
7. Visualize Percentages: Some people find it helpful to visualize percentages using diagrams or charts. For example, you can use a pie chart to represent the different components of a budget, with each slice representing a percentage of the total budget.
- Tip: Use different colors to represent different percentages in your visualizations to make them easier to understand.
8. Don't Be Afraid to Break Down Complex Problems: If you're facing a complex percentage problem, break it down into smaller, more manageable steps. For example, if you're calculating a series of discounts, calculate each discount separately and then combine the results.
- Example: To calculate the final price after a 20% discount followed by a 10% discount, first calculate the price after the 20% discount, and then apply the 10% discount to that new price.
9. Practice Regularly: Like any skill, mastering percentages requires regular practice. Set aside some time each week to work on percentage problems, and gradually increase the difficulty of the problems as you become more comfortable.
- Resource: Use online resources, textbooks, and practice worksheets to find a variety of percentage problems to solve.
10. Seek Help When Needed: If you're struggling with percentages, don't be afraid to seek help from teachers, tutors, or online forums. There are many resources available to help you improve your understanding and skills.
- Remember: Asking for help is a sign of strength, not weakness.
By following these practical tips and expert advice, you can develop a strong understanding of percentages and apply them confidently to a wide range of situations.
Frequently Asked Questions (FAQ)
Q: What is the difference between a percentage and a percentile?
A: A percentage expresses a proportion out of 100, while a percentile indicates the value below which a given percentage of observations in a group of observations fall. For example, scoring in the 90th percentile on a test means you scored higher than 90% of the other test-takers.
Q: How do I calculate percentage increase or decrease?
A: Percentage Increase/Decrease = [(New Value - Old Value) / Old Value] * 100. A positive result indicates an increase, while a negative result indicates a decrease.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when comparing a new value to an original value and the new value is more than double the original. For example, if a company's sales increased by 150%, it means their sales are now 2.5 times higher than they were before.
Q: How do I calculate a percentage of a percentage?
A: To calculate a percentage of a percentage, convert both percentages to decimals and then multiply them. For example, 20% of 50% is 0.20 * 0.50 = 0.10, which is 10%.
Q: Why are percentages so widely used?
A: Percentages are widely used because they provide a standardized and easily understandable way to express proportions. They allow for quick comparison across different datasets and are applicable in various fields, from finance and statistics to everyday shopping and cooking.
Conclusion
Calculating what percent 19 is of 25, as we've explored, is a fundamental skill that extends far beyond basic arithmetic. It's a key to understanding proportions, making informed decisions, and navigating a world increasingly driven by data. By mastering the basic formula, understanding the nuances of percentage-related problems, and practicing regularly, you can unlock the power of percentages and apply them confidently to a wide range of situations.
From understanding discounts at the store to interpreting statistical data in news articles, the ability to work with percentages empowers you to make informed decisions and critically evaluate information. Embrace the challenge, practice consistently, and you'll find that percentages become an invaluable tool in your everyday life. Now, take what you've learned and apply it to the world around you. Calculate that tip, analyze that data, and empower yourself with the knowledge of percentages. What are you waiting for? Go calculate!
Latest Posts
Latest Posts
-
Determine The Volume Of The Shaded Region
Nov 28, 2025
-
Parts Of A Sewing Machine Diagram
Nov 28, 2025
-
What Is 2 To The Power Of 4
Nov 28, 2025
-
60 Is What Percent Of 12
Nov 28, 2025
-
What Does Regrouping Mean In Math
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 19 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.