What Percent Is 5 Of 20
sandbardeewhy
Nov 23, 2025 · 9 min read
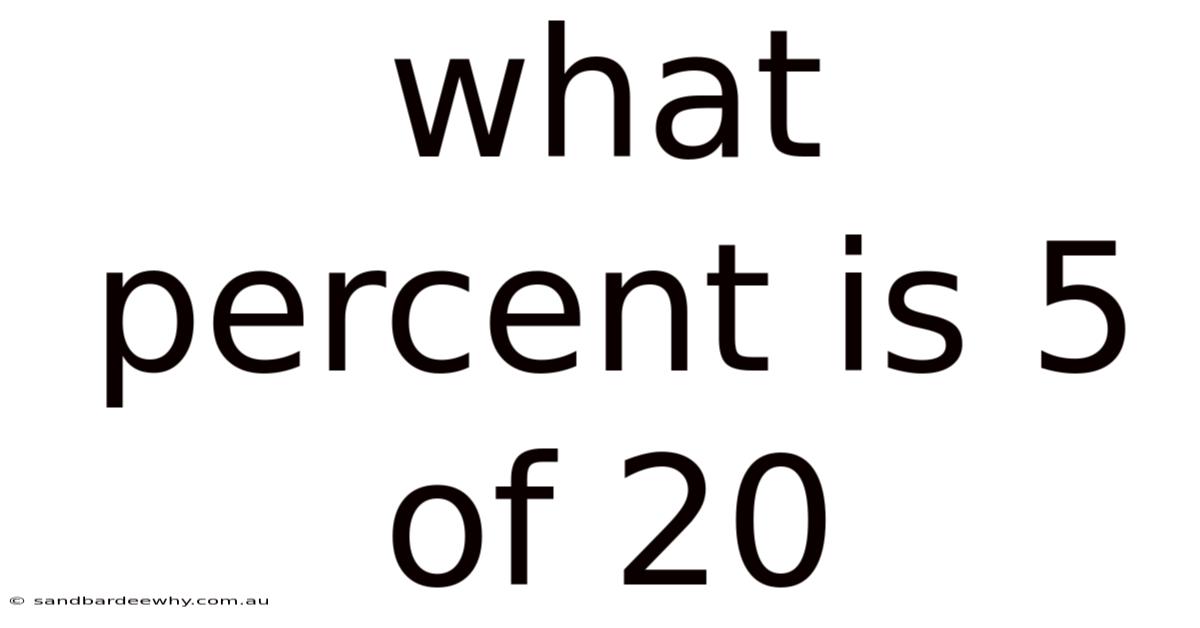
Table of Contents
Imagine you're at a bustling farmer's market, eyeing a basket overflowing with twenty ripe, juicy apples. As you reach in, you pick out five of these perfect specimens. The question that might naturally arise is: What portion of the entire basket have you selected? How do we express this selection as a percentage, a common language for proportions?
In our daily lives, percentages are all around us. From calculating discounts at our favorite stores to understanding the breakdown of ingredients in a recipe, percentages provide a simple way to represent fractions and proportions. Figuring out "what percent is 5 of 20" isn't just a math problem; it's a practical skill that helps us make sense of the world.
Unveiling the Percentage: What Percent is 5 of 20?
Percentages are a fundamental part of mathematics, used extensively in everyday life to understand proportions, ratios, and changes. Calculating "what percent is 5 of 20" is a basic yet essential skill. This article aims to comprehensively break down the concept, explore its applications, and provide a clear understanding of how to calculate percentages effectively.
Comprehensive Overview
Definition of Percentage
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "per hundred." In simpler terms, a percentage tells you how many parts out of 100 you have. It is denoted by the symbol "%". For example, 50% means 50 out of 100, or one-half.
The Scientific Foundation
The concept of percentages is rooted in basic arithmetic and proportional reasoning. At its core, a percentage is a ratio that has been scaled to a base of 100. The formula to calculate a percentage is:
Percentage = (Part / Whole) * 100
Here, the "part" is the specific quantity you're interested in, and the "whole" is the total quantity or the reference value. Multiplying the ratio of the part to the whole by 100 converts it into a percentage. This scaling to 100 allows for easy comparison and understanding across different contexts.
History of Percentages
The use of percentages can be traced back to ancient Rome, where Emperor Augustus levied a tax of 1/100 on goods sold at auction. This was equivalent to 1%. However, the modern concept of percentages as we know it today developed during the Renaissance. As trade and commerce flourished, there was an increasing need for a standardized way to calculate interest rates, profits, and losses.
By the 15th century, mathematicians began using percentages regularly. The first known explicit use of the percent sign (%) appeared in the 17th century. Over time, percentages became an indispensable tool in finance, statistics, and everyday calculations.
Essential Concepts
To fully grasp how to calculate "what percent is 5 of 20," it's important to understand a few key concepts:
- Base: The base is the total or whole quantity. In our example, 20 is the base.
- Part: The part is the specific quantity being compared to the base. In our example, 5 is the part.
- Percentage: The percentage is the value that expresses the part as a fraction of the whole, multiplied by 100.
Applying the Formula to "What Percent is 5 of 20"
Now, let's apply the percentage formula to our original question: "What percent is 5 of 20?"
-
Identify the Part and the Whole:
- Part = 5
- Whole = 20
-
Apply the Formula:
- Percentage = (Part / Whole) * 100
- Percentage = (5 / 20) * 100
-
Calculate:
- Percentage = 0.25 * 100
- Percentage = 25%
Therefore, 5 is 25% of 20.
The Importance of a Solid Mathematical Foundation
Understanding percentages requires a solid foundation in basic mathematical operations such as division and multiplication. It's crucial to be comfortable with fractions and decimals, as these are often used interchangeably with percentages. For instance, 25% is equivalent to the fraction 1/4 and the decimal 0.25. Being able to convert between these forms is essential for solving percentage-related problems efficiently.
Real-World Applications
Percentages are used extensively in various fields, highlighting their practical importance. Here are a few examples:
- Finance: Calculating interest rates on loans, returns on investments, and profit margins in business.
- Retail: Determining discounts on products, calculating sales tax, and understanding markup percentages.
- Statistics: Representing data in a meaningful way, such as the percentage of people who support a particular political candidate or the percentage of students who passed an exam.
- Health: Expressing body fat percentage, calculating medication dosages, and understanding the effectiveness of treatments.
Visual Aids and Tools
Visual aids, such as pie charts and bar graphs, are often used to represent percentages, making it easier to understand and interpret data. Pie charts are particularly useful for showing how a whole is divided into different parts, each represented as a percentage. Bar graphs, on the other hand, are helpful for comparing percentages across different categories.
Trends and Latest Developments
Increased Use in Data Analysis
In recent years, there has been a significant increase in the use of percentages in data analysis. With the rise of big data and the need to make sense of large datasets, percentages provide a simple and effective way to summarize and communicate findings. Data analysts often use percentages to identify trends, compare performance metrics, and make informed decisions.
Percentages in Social Media and Marketing
Percentages play a crucial role in social media and digital marketing. Marketers use percentages to track the success of their campaigns, measure engagement rates, and analyze customer behavior. For example, click-through rates (CTR), conversion rates, and bounce rates are all expressed as percentages, providing valuable insights into the effectiveness of marketing strategies.
Popular Opinions and Surveys
Percentages are a staple in opinion polls and surveys. Whether it's gauging public sentiment on political issues or understanding consumer preferences for products, percentages are used to present the results in a clear and concise manner. This allows for easy comparison and understanding of the data, making it accessible to a wide audience.
Professional Insights
From a professional perspective, understanding percentages is not just about knowing the formula; it's about being able to interpret and apply the results in a meaningful way. For example, when analyzing financial statements, it's important to understand how percentage changes in revenue or expenses impact the overall profitability of a company. Similarly, in project management, tracking progress as a percentage of completion can help ensure that projects stay on schedule and within budget.
The Role of Technology
Technology has made it easier than ever to calculate and work with percentages. Spreadsheets, calculators, and online tools can quickly perform complex percentage calculations, saving time and reducing the risk of errors. These tools also allow for easy visualization of percentage data through charts and graphs, further enhancing understanding and communication.
Tips and Expert Advice
Tip 1: Practice Regularly
The best way to master percentages is to practice regularly. Start with simple problems and gradually increase the complexity. Work through real-world examples and try to apply percentages in your daily life. For instance, when shopping, calculate the discount you're receiving as a percentage of the original price.
Regular practice helps to build confidence and reinforces the understanding of the underlying concepts. It also allows you to develop problem-solving skills and learn how to approach different types of percentage-related questions.
Tip 2: Understand the Context
Always pay attention to the context of the problem. Understanding what the base and the part represent is crucial for setting up the calculation correctly. Misinterpreting the context can lead to incorrect results, even if the calculation itself is accurate.
For example, if a store offers a 20% discount on a product, it's important to understand whether the discount is applied before or after taxes. This can significantly impact the final price you pay.
Tip 3: Use Estimation
Before performing a precise calculation, try to estimate the answer. This can help you catch errors and ensure that your final result is reasonable. For instance, if you're calculating what percent is 5 of 20, you might estimate that it's around 25%, since 5 is one-fourth of 20.
Estimation also helps to develop a better understanding of the relative sizes of different quantities. It encourages you to think critically about the problem and make informed judgments.
Tip 4: Break Down Complex Problems
Complex percentage problems can often be broken down into simpler steps. Identify the individual components and solve them one at a time. This approach makes the problem more manageable and reduces the likelihood of errors.
For example, if you're calculating a series of discounts, calculate each discount separately and then apply them sequentially to the original price.
Tip 5: Double-Check Your Work
Always double-check your work to ensure accuracy. Review your calculations and make sure that you have used the correct formula and values. This is particularly important in situations where errors can have significant consequences, such as in financial calculations.
Using a calculator or spreadsheet can help to reduce the risk of errors, but it's still important to verify the results manually.
FAQ
Q: What is the formula for calculating a percentage?
A: The formula for calculating a percentage is: Percentage = (Part / Whole) * 100
Q: How do you convert a percentage to a decimal?
A: To convert a percentage to a decimal, divide the percentage by 100. For example, 25% = 25 / 100 = 0.25.
Q: How do you convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.75 = 0.75 * 100 = 75%.
Q: What is the difference between a percentage increase and a percentage decrease?
A: A percentage increase represents the relative increase in a quantity, while a percentage decrease represents the relative decrease. The formulas are:
- Percentage Increase = ((New Value - Old Value) / Old Value) * 100
- Percentage Decrease = ((Old Value - New Value) / Old Value) * 100
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when the part is greater than the whole. For example, if a company's revenue doubles, the percentage increase would be 100%.
Conclusion
In summary, understanding how to calculate "what percent is 5 of 20" is a fundamental skill with broad applications across various fields. By grasping the definition of percentage, understanding its historical roots, and practicing regularly, anyone can master this essential concept. Remember, percentages are a tool for understanding proportions, making informed decisions, and communicating information effectively.
Ready to put your knowledge to the test? Try calculating percentages in your daily life – from discounts while shopping to understanding statistics in the news. Share your experiences and any challenges you face in the comments below. Let's continue to enhance our understanding of percentages together!
Latest Posts
Latest Posts
-
Summary To Kill A Mockingbird Chapter 9
Nov 23, 2025
-
What Is The Theme Of The Crucible
Nov 23, 2025
-
How Long Is The Skyway Bridge
Nov 23, 2025
-
What Percent Is 5 Of 20
Nov 23, 2025
-
What Is The Purpose Of Cholesterol In The Plasma Membrane
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 5 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.