What Percent Is 8 Out Of 12
sandbardeewhy
Nov 23, 2025 · 12 min read
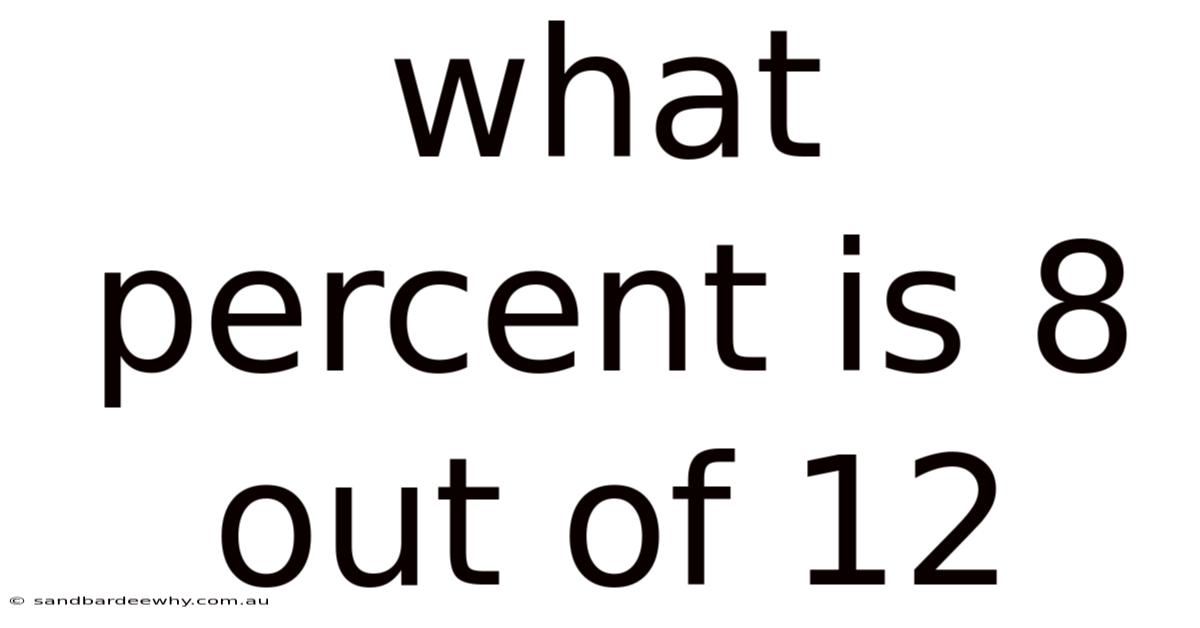
Table of Contents
Imagine you're at a pizza party, and the host proudly announces they've ordered 12 slices. You eagerly anticipate your share, and when the dust settles, you've managed to snag 8 slices. While savoring the delicious pizza, a thought pops into your head: "What percentage of the whole pizza did I just devour?" This simple scenario highlights a common need: understanding how to calculate percentages in everyday situations.
Calculating percentages is more than just a mathematical exercise; it's a fundamental skill with broad applications in finance, statistics, and daily life. From figuring out discounts at your favorite store to understanding your investment returns, knowing how to determine what percent a number is of another is incredibly useful. In our pizza example, we want to determine what percent is 8 out of 12. This skill not only satisfies our curiosity but also empowers us to make informed decisions and analyze data more effectively.
The Basics of Percentage Calculation
To understand what percent is 8 out of 12, let's delve into the fundamentals of percentage calculations. The term "percent" comes from the Latin per centum, meaning "per hundred." A percentage is essentially a way of expressing a number as a fraction of 100. It's a standardized way to represent proportions, making it easy to compare different ratios and quantities.
Definition of Percentage
A percentage is a ratio or proportion expressed as a fraction of 100. It's a dimensionless number, meaning it doesn't have any units of measurement. We use the percent symbol "%" to denote that a number is a percentage. For example, 50% represents 50 out of 100, or half of a whole.
Formula for Calculating Percentage
The basic formula for calculating a percentage is:
Percentage = (Part / Whole) × 100
Here, "Part" refers to the specific quantity you're interested in, and "Whole" refers to the total or reference quantity. By dividing the part by the whole and multiplying the result by 100, you convert the ratio into a percentage. This formula is the cornerstone for understanding how to determine what percent is a number of another.
Applying the Formula to "What Percent is 8 out of 12?"
Now, let's apply the formula to our initial question: "What percent is 8 out of 12?"
- Part = 8
- Whole = 12
Plugging these values into the formula, we get:
Percentage = (8 / 12) × 100
First, divide 8 by 12: 8 / 12 = 0.6667 (approximately)
Next, multiply this result by 100: 0. 6667 × 100 = 66.67%
Therefore, 8 is approximately 66.67% of 12.
Historical Context of Percentage
The concept of percentages dates back to ancient Rome, where calculations were often made in terms of fractions of 100, particularly in relation to taxes and trade. However, the modern use of the percent symbol (%) and the widespread application of percentage calculations became more prevalent during the Renaissance. Merchants, bankers, and scientists needed a standardized way to express ratios and proportions, and percentages provided a convenient solution.
Over time, percentages became an indispensable tool in various fields, including finance, economics, statistics, and science. They allow for easy comparison of data, assessment of growth rates, and analysis of trends. The simplicity and universality of percentages have made them a fundamental part of quantitative reasoning and decision-making.
Understanding the Components: Base, Rate, and Percentage
In percentage calculations, it's crucial to understand the roles of the base, rate, and percentage.
- Base: The base is the whole or total quantity to which the percentage refers. In our example, 12 is the base because it's the total number of slices.
- Rate: The rate is the percentage itself, expressed as a number out of 100. In our example, the rate is what we're trying to find.
- Percentage: The percentage is the part of the base that we're interested in. In our example, 8 is the percentage because it's the number of slices we have.
These components are interconnected, and understanding their relationship is key to solving percentage problems accurately. The formula that ties them together is:
Percentage = Base × Rate
By rearranging this formula, you can solve for any of the components if you know the other two. For instance, if you know the percentage and the base, you can find the rate by dividing the percentage by the base and multiplying by 100.
Common Mistakes to Avoid
When calculating percentages, it's essential to avoid common mistakes that can lead to inaccurate results. One frequent error is confusing the part and the whole. Always make sure you correctly identify which quantity is the part and which is the whole. For example, if the question is "What percent is 30 of 200?", ensure that 30 is treated as the part and 200 as the whole.
Another common mistake is forgetting to multiply by 100. The purpose of multiplying by 100 is to convert the ratio into a percentage. Without this step, you'll end up with a decimal or fraction instead of a percentage.
Additionally, be mindful of rounding errors. When dealing with decimals, it's often necessary to round the result. However, rounding too early in the calculation can lead to significant errors in the final percentage. It's best to perform the rounding at the end of the calculation to maintain accuracy.
Real-World Applications of Percentage Calculations
Percentage calculations are used extensively in various real-world scenarios. In finance, they're used to calculate interest rates, investment returns, and profit margins. For example, if you invest $1,000 in a stock and it grows to $1,100 in a year, the percentage return on your investment is:
Percentage Return = (($1,100 - $1,000) / $1,000) × 100 = 10%
In retail, percentages are used to calculate discounts, sales tax, and markups. For instance, if an item originally priced at $50 is on sale for 20% off, the discount amount is:
Discount Amount = $50 × (20 / 100) = $10
The sale price is then $50 - $10 = $40.
In statistics, percentages are used to represent proportions and probabilities. For example, if a survey of 500 people finds that 350 prefer coffee over tea, the percentage of people who prefer coffee is:
Percentage = (350 / 500) × 100 = 70%
These examples illustrate the versatility and practicality of percentage calculations in everyday life.
Trends and Latest Developments
The way we use percentages is evolving with technological advancements and changing data landscapes. Here's a look at some current trends and developments:
Data Visualization
With the explosion of big data, data visualization has become an essential tool for presenting complex information in an understandable format. Percentages play a crucial role in these visualizations, often used in pie charts, bar graphs, and other visual representations to convey proportions and distributions. Tools like Tableau, Power BI, and Python libraries such as Matplotlib and Seaborn make it easier to create compelling data visualizations that highlight key percentage-based insights.
Machine Learning and AI
Machine learning algorithms often rely on percentages to evaluate model performance. For example, accuracy, precision, and recall are all percentage-based metrics used to assess how well a model is performing. In AI applications, percentages can be used to quantify the confidence level of a prediction or decision. For instance, a self-driving car might use percentages to express the probability of a pedestrian crossing the road.
Financial Technology (FinTech)
In FinTech, percentages are at the heart of many applications. Robo-advisors use algorithms to manage investments, often presenting portfolio allocations and performance metrics as percentages. Cryptocurrency platforms use percentages to display price changes, trading volumes, and market capitalization. Understanding these percentage-based metrics is crucial for making informed financial decisions in the digital age.
E-commerce and Marketing
E-commerce platforms heavily rely on percentages to drive sales and marketing strategies. Conversion rates, click-through rates, and bounce rates are all percentage-based metrics used to evaluate the effectiveness of online campaigns. Retailers use personalized discounts and promotions, often expressed as percentages, to incentivize purchases and build customer loyalty.
Professional Insights
As data becomes more pervasive, professionals need to be adept at interpreting and communicating percentage-based insights. In finance, analysts use percentage changes to assess the performance of stocks and bonds. In marketing, professionals use percentage lift to measure the impact of a new campaign. In healthcare, researchers use percentages to report the effectiveness of treatments and interventions.
Staying up-to-date with these trends requires continuous learning and adaptation. Professionals should focus on developing skills in data analysis, visualization, and communication to effectively leverage percentages in their respective fields.
Tips and Expert Advice
Calculating percentages accurately and efficiently can be a valuable skill in many aspects of life. Here are some tips and expert advice to help you master percentage calculations:
Simplify Fractions
Before calculating a percentage, try to simplify the fraction as much as possible. Simplifying the fraction can make the division easier and reduce the chances of making errors. For example, if you're trying to find what percent is 15 out of 25, you can simplify the fraction 15/25 to 3/5. This makes the division step easier:
3 / 5 = 0.6
Then, multiply by 100: 0. 6 × 100 = 60%
Simplifying fractions can save time and improve accuracy, especially when dealing with larger numbers.
Use Benchmarks
Familiarize yourself with common percentage benchmarks, such as 25%, 50%, and 75%. These benchmarks can help you quickly estimate percentages and check the reasonableness of your calculations. For example, if you need to find what percent is 48 out of 100, you can quickly recognize that it's close to 50%, which is half of the whole. This can help you catch any significant errors in your calculation.
Estimate First
Before performing the calculation, take a moment to estimate the percentage. This can help you develop a sense of whether your final answer is reasonable. For example, if you're trying to find what percent is 3 out of 20, you might estimate that it's around 15% because 3 is a little more than 1/6 of 20. Then, when you perform the calculation:
3 / 20 = 0.15 0. 15 × 100 = 15%
Your estimate helps you confirm that your answer is in the right ballpark.
Double-Check Your Work
Always double-check your work to ensure accuracy. Percentage calculations can be prone to errors, so it's important to verify your results. One way to double-check is to use a different method to calculate the percentage. For example, if you used the formula (Part / Whole) × 100, you can also use a proportion:
Part / Whole = Percentage / 100
Solve for the percentage to verify your answer.
Use Technology
Take advantage of technology to calculate percentages quickly and accurately. Calculators, spreadsheets, and online percentage calculators can help you perform calculations with ease. Spreadsheets like Microsoft Excel and Google Sheets have built-in functions for calculating percentages, such as the PERCENT function. Online calculators are readily available and can be useful for quick calculations on the go.
Practice Regularly
The more you practice percentage calculations, the more comfortable and confident you'll become. Try to incorporate percentage calculations into your daily life, such as when calculating tips at restaurants, figuring out discounts while shopping, or tracking your personal finances. Regular practice will help you develop a strong intuition for percentages and improve your accuracy and speed.
Understand the Context
Always consider the context of the percentage calculation. Percentages can be easily misinterpreted if taken out of context. For example, a 10% increase might seem significant, but if the base is very small, the actual increase might be negligible. Similarly, a 50% decrease might seem large, but if the base was very high, the remaining amount might still be substantial. Understanding the context is crucial for interpreting percentages accurately and making informed decisions.
Use Visual Aids
Visual aids like pie charts and bar graphs can help you understand and communicate percentages more effectively. Visualizing percentages can make it easier to grasp the relative proportions and relationships between different quantities. Tools like Tableau and Power BI can help you create visually appealing and informative charts that highlight key percentage-based insights.
FAQ
Q: What is the formula for calculating percentage? A: The formula for calculating percentage is: Percentage = (Part / Whole) × 100.
Q: How do I convert a decimal to a percentage? A: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.75 becomes 75%.
Q: How do I find the percentage increase or decrease? A: To find the percentage increase or decrease, use the formula: Percentage Change = ((New Value - Old Value) / Old Value) × 100. If the result is positive, it's an increase; if it's negative, it's a decrease.
Q: What's the difference between percentage and percentage points? A: Percentage is a proportion out of 100, while percentage points refer to the difference between two percentages. For example, if a value increases from 10% to 15%, it's an increase of 5 percentage points.
Q: How do I calculate percentage of a number? A: To calculate the percentage of a number, multiply the number by the percentage (expressed as a decimal). For example, to find 20% of 50, multiply 50 by 0.20, which equals 10.
Conclusion
Understanding what percent is 8 out of 12—or any number out of another—is a fundamental skill with broad applications in various fields. By grasping the basic formula, avoiding common mistakes, and applying practical tips, you can master percentage calculations and make informed decisions in both your personal and professional life. From finance and retail to statistics and technology, percentages are an indispensable tool for analyzing data, assessing proportions, and communicating insights.
Now that you've gained a comprehensive understanding of percentage calculations, take the next step and apply this knowledge to real-world scenarios. Whether you're calculating discounts while shopping, tracking your investment returns, or analyzing data at work, the ability to calculate percentages accurately and efficiently will empower you to make better decisions and achieve your goals. Practice regularly, stay curious, and continue to explore the fascinating world of percentages!
Latest Posts
Latest Posts
-
How Many Years Is 22 Months
Nov 23, 2025
-
What Is The Properties Of Math
Nov 23, 2025
-
What Is The Setting For The Outsiders
Nov 23, 2025
-
How Many Ounces Are In 2 Pints
Nov 23, 2025
-
What Percent Is 8 Out Of 12
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 8 Out Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.