What Percent Of 5 Is 20
sandbardeewhy
Nov 28, 2025 · 12 min read
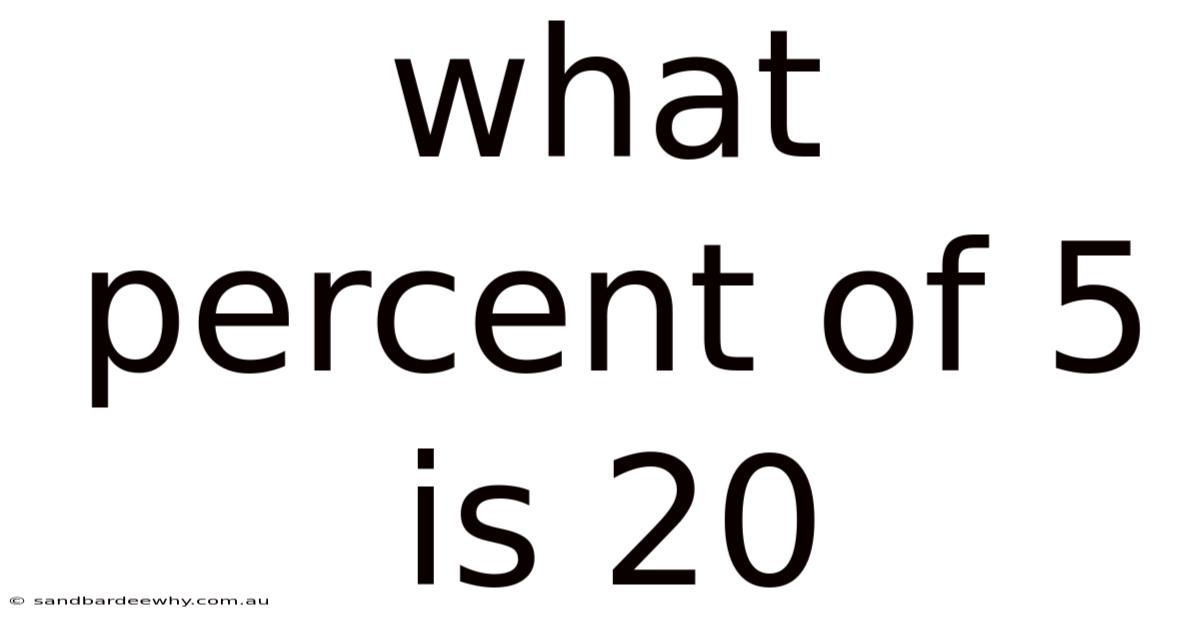
Table of Contents
Imagine you're at a bustling farmer's market, surrounded by vibrant colors and enticing aromas. A vendor offers you a sweet deal: "20 apples for the price of 5!" Intrigued, you wonder, "What percentage increase is that?" This simple question takes us to the heart of understanding percentages, proportions, and the relationship between numbers. Calculating percentages isn't just a math exercise; it's a skill that empowers us to make informed decisions in everyday life, from understanding discounts to analyzing statistical data.
Have you ever felt lost trying to calculate a tip at a restaurant or decode the interest rate on a loan? Percentages are a fundamental part of our daily financial interactions, scientific analyses, and even understanding sports statistics. Knowing how to calculate what percent of 5 is 20 might seem basic, but it unlocks a deeper understanding of proportional thinking. It's about seeing the relationship between numbers, understanding ratios, and converting them into a universally understandable format—percentages. This article will guide you through the process, provide real-world examples, and offer expert advice to master percentage calculations.
Main Subheading
Percentages are a ubiquitous tool in various fields, including finance, statistics, and everyday life. Understanding percentages is crucial for making informed decisions, whether you're calculating discounts, analyzing data, or determining proportions. The question "What percent of 5 is 20?" is a fundamental exercise in understanding how percentages work and how to calculate them accurately.
At its core, calculating percentages involves understanding the relationship between two numbers and expressing that relationship as a fraction of 100. The concept is relatively straightforward, but its applications are vast and varied. From determining the growth rate of a business to understanding the composition of a chemical compound, percentages provide a standardized way to compare and interpret data. They help simplify complex information, making it easier to understand and communicate. Mastering percentage calculations enables us to navigate a world filled with numerical data with confidence and precision.
Comprehensive Overview
Definition of Percentage
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." It is denoted by the symbol "%." In mathematical terms, a percentage represents a ratio that has been scaled to have a denominator of 100. This allows for easy comparison and understanding of proportions.
For instance, if we say 50%, we mean 50 out of 100, or 50/100. This can be simplified to 1/2, indicating that 50% represents half of the whole. Similarly, 25% means 25 out of 100, or 25/100, which simplifies to 1/4, representing a quarter of the whole. Understanding this foundational concept is crucial for performing percentage calculations accurately and applying them in various contexts.
Scientific Foundations
The mathematical basis of percentages lies in the principles of ratios and proportions. A ratio is a comparison of two quantities, while a proportion is an equality between two ratios. When we calculate a percentage, we are essentially finding a proportion where one of the ratios has a denominator of 100.
The formula to calculate what percent a number A is of a number B is:
Percentage = (A / B) * 100
This formula is derived from the basic principles of algebra. By dividing A by B, we find the ratio of A to B. Multiplying this ratio by 100 converts it into a percentage, allowing us to express the relationship between A and B in terms of parts per hundred. This method ensures that percentages can be easily compared and understood across different scales and contexts.
History of Percentages
The concept of percentages has ancient roots, tracing back to the Roman Empire. The Romans often levied taxes expressed as fractions of assets, such as 1/100, which was referred to as centesima. However, the modern concept of percentages as we know it today developed during the Middle Ages.
During the 15th century, as trade and commerce flourished, the use of percentages became more widespread in Europe. Merchants needed a standardized way to calculate profits, losses, and interest rates. The introduction of the decimal system further facilitated the use of percentages, as it allowed for easier calculations and comparisons. By the 17th century, percentages were an integral part of mathematical education and were widely used in various fields, including finance, statistics, and science.
Essential Concepts
To effectively work with percentages, it's important to understand several key concepts:
- Base: The base is the whole amount or the reference value to which the percentage is applied. In the question "What percent of 5 is 20?", the base is 5.
- Percentage: The percentage is the proportion or rate expressed as a fraction of 100. It represents how many parts of the base are being considered.
- Amount: The amount is the portion of the base that is being calculated or compared. In the question "What percent of 5 is 20?", the amount is 20.
Understanding the relationship between these components is essential for correctly setting up and solving percentage problems. For example, if we want to find 20% of 50, 50 is the base, 20% is the percentage, and we are trying to find the amount.
Calculating "What Percent of 5 is 20?"
To calculate what percent of 5 is 20, we use the formula:
Percentage = (A / B) * 100
In this case, A is 20 and B is 5. Plugging these values into the formula, we get:
Percentage = (20 / 5) * 100
First, divide 20 by 5:
20 / 5 = 4
Next, multiply the result by 100:
4 * 100 = 400
Therefore, 20 is 400% of 5. This means that 20 is four times greater than 5, expressed as a percentage.
Trends and Latest Developments
Current Trends in Percentage Usage
Percentages remain a fundamental tool in various sectors, and their application continues to evolve with advancements in technology and data analytics. In finance, percentages are used to calculate interest rates, investment returns, and risk assessments. Retailers use percentages to determine discounts, markups, and profit margins. In healthcare, percentages are used to track patient outcomes, measure the effectiveness of treatments, and analyze epidemiological data.
With the rise of big data and data science, percentages are increasingly used in statistical analysis and machine learning. Data scientists use percentages to summarize and interpret large datasets, identify trends, and make predictions. Visualizing data using percentages helps stakeholders understand complex information quickly and make informed decisions.
Data and Statistics
Recent data indicates that numeracy skills, including the ability to work with percentages, are increasingly important in the modern workforce. Studies show that individuals with strong numeracy skills are more likely to secure higher-paying jobs and manage their finances effectively. Educational institutions and employers are placing greater emphasis on numeracy training to ensure that individuals have the skills necessary to succeed in a data-driven world.
According to a report by the National Numeracy organization, a significant portion of the adult population struggles with basic percentage calculations. This highlights the need for continued education and awareness to improve numeracy skills and empower individuals to make informed decisions in their daily lives.
Popular Opinions
There is a general consensus that understanding percentages is an essential life skill. Many people believe that basic numeracy should be a core component of education, starting from primary school. Parents, educators, and policymakers recognize the importance of equipping students with the skills they need to navigate a world filled with numerical data.
However, some argue that the traditional methods of teaching percentages can be overly complex and confusing. There is a growing movement towards more practical, hands-on approaches to teaching numeracy, focusing on real-world applications and problem-solving. This shift aims to make learning percentages more engaging and relevant for students of all ages.
Professional Insights
Experts in mathematics education emphasize the importance of conceptual understanding over rote memorization when teaching percentages. They recommend using visual aids, such as diagrams and manipulatives, to help students grasp the underlying principles of percentage calculations. Real-world examples and interactive activities can also make learning more meaningful and engaging.
Financial advisors stress the importance of understanding percentages for making informed investment decisions. They advise individuals to pay close attention to interest rates, investment returns, and fees, which are often expressed as percentages. Understanding these figures can help investors make sound financial choices and achieve their long-term goals.
Tips and Expert Advice
Practical Advice for Accurate Calculations
- Understand the Base:
- Always identify the base value correctly. The base is the reference point from which the percentage is calculated. In the question "What percent of 5 is 20?", the base is 5. Confusing the base can lead to incorrect calculations.
- Example: If you're calculating a discount, the original price is the base. If you're calculating a percentage increase, the starting value is the base.
- Use the Correct Formula:
- Ensure you're using the correct formula for the calculation you're performing. The basic formula for finding what percent A is of B is:
Percentage = (A / B) * 100. - Example: To find what percent 30 is of 200, use the formula:
(30 / 200) * 100 = 15%.
- Ensure you're using the correct formula for the calculation you're performing. The basic formula for finding what percent A is of B is:
- Convert Percentages to Decimals or Fractions:
- To perform calculations involving percentages, it's often easier to convert them to decimals or fractions. To convert a percentage to a decimal, divide by 100. To convert a percentage to a fraction, write the percentage as a fraction with a denominator of 100 and simplify.
- Example: 25% is equal to 0.25 as a decimal and 1/4 as a fraction.
- Check Your Work:
- Always double-check your calculations to ensure accuracy. A small error can lead to significant discrepancies, especially in financial or statistical contexts.
- Example: If you calculate a 20% discount on a $100 item to be $10, you've made an error. The correct discount is $20.
Real-World Examples
- Finance:
- Calculating interest rates on loans or investments. If you invest $1,000 and earn $50 in interest, the return on investment is (50 / 1000) * 100 = 5%.
- Understanding discounts and markups. A store offering a 30% discount on a $200 item means the price is reduced by $200 * 0.30 = $60, making the final price $140.
- Retail:
- Determining profit margins. If a product costs $50 to produce and sells for $80, the profit margin is ((80 - 50) / 50) * 100 = 60%.
- Analyzing sales growth. If sales increase from $10,000 in January to $12,000 in February, the growth rate is ((12000 - 10000) / 10000) * 100 = 20%.
- Science and Statistics:
- Analyzing experimental data. If an experiment shows a 15% improvement in results compared to a control group, this indicates the effectiveness of the experimental treatment.
- Calculating error rates. If a machine produces 5 defective items out of 500, the error rate is (5 / 500) * 100 = 1%.
- Daily Life:
- Calculating tips at restaurants. A 15% tip on a $40 bill is $40 * 0.15 = $6.
- Understanding nutritional information. If a food label indicates that a serving contains 20% of the daily recommended intake of fat, it means that serving provides 20% of the total fat you should consume in a day.
Expert Advice for Mastering Percentages
- Practice Regularly:
- The more you practice percentage calculations, the more comfortable and confident you'll become. Use online resources, textbooks, and real-world scenarios to hone your skills.
- Visualize Percentages:
- Use visual aids like pie charts, bar graphs, and diagrams to understand how percentages relate to the whole. Visualizing percentages can make abstract concepts more concrete and easier to grasp.
- Break Down Complex Problems:
- When faced with a complex percentage problem, break it down into smaller, more manageable steps. Identify the base, the percentage, and the amount, and then apply the appropriate formula.
- Use Technology Wisely:
- Utilize calculators and spreadsheet software to perform percentage calculations quickly and accurately. However, make sure you understand the underlying principles before relying solely on technology.
- Seek Help When Needed:
- Don't hesitate to ask for help from teachers, tutors, or online resources if you're struggling with percentage calculations. Understanding percentages is a foundational skill that will benefit you in many areas of life.
FAQ
Q: What is the formula for calculating what percent of a number A is of a number B?
A: The formula is Percentage = (A / B) * 100.
Q: How do I convert a percentage to a decimal? A: Divide the percentage by 100. For example, 25% becomes 0.25.
Q: How do I find the amount if I know the percentage and the base? A: Multiply the base by the percentage (expressed as a decimal). For example, 20% of 50 is 50 * 0.20 = 10.
Q: Why are percentages important? A: Percentages provide a standardized way to compare and interpret data, making it easier to understand proportions and make informed decisions in various fields, including finance, statistics, and everyday life.
Q: What are common mistakes to avoid when calculating percentages? A: Common mistakes include confusing the base value, using the wrong formula, and not checking your work.
Conclusion
Understanding what percent of 5 is 20, and more broadly, how percentages work, is a crucial skill that empowers you to make informed decisions in various aspects of life. By mastering the basic formula, understanding the concepts of base and amount, and practicing regularly, you can confidently tackle percentage problems in finance, retail, science, and daily life. Remember, the formula to find what percent of 5 is 20 is (20 / 5) * 100 = 400%.
Now that you have a solid understanding of percentages, take the next step and apply your knowledge to real-world scenarios. Whether you're calculating discounts, analyzing data, or managing your finances, the ability to work with percentages will serve you well. Share this article with friends and family to help them improve their numeracy skills and confidently navigate a world filled with numerical data.
Latest Posts
Latest Posts
-
What Percent Of 20 Is 7
Nov 28, 2025
-
What Is A Bunch Of Horses Called
Nov 28, 2025
-
Domain And Range Of The Trigonometric Functions
Nov 28, 2025
-
Why Would A Cell Need To Divide
Nov 28, 2025
-
What Temp Does Water Freeze Celsius
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 5 Is 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.