What Percent Of 50 Is 6
sandbardeewhy
Nov 26, 2025 · 9 min read
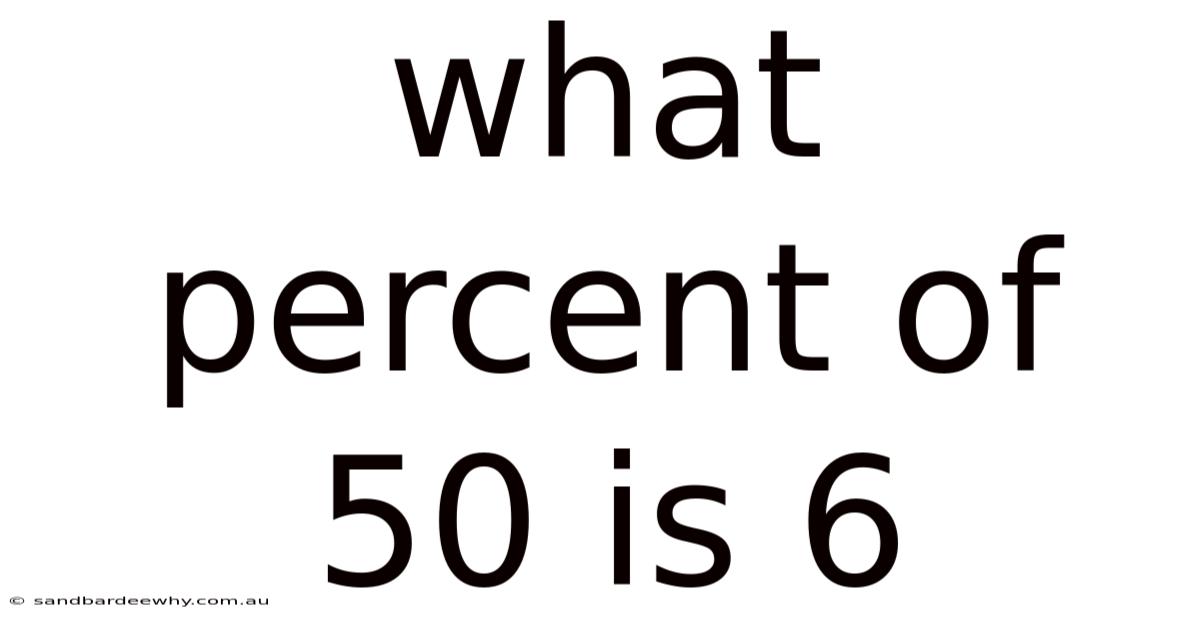
Table of Contents
Imagine you're at a bustling farmer's market, eyeing a vibrant display of apples. The vendor announces a special: "12% off any purchase over $50!" You pick out a basket brimming with crisp, red apples totaling exactly $50. As you approach the counter, you quickly calculate the discount in your head – $6! That mental math you just performed is essentially what we're going to explore: figuring out what percentage one number represents of another.
Calculating percentages is a fundamental skill that transcends everyday scenarios like shopping discounts. It's a cornerstone of financial analysis, scientific research, and countless other fields. Whether you're determining sales tax, analyzing profit margins, or understanding statistical data, grasping the concept of percentages is absolutely essential. So, let's break down the question: what percent of 50 is 6?
Understanding Percentage Calculations
To determine what percent of 50 is 6, we're essentially asking: "6 is what fraction of 50, expressed as a percentage?" This involves a simple but powerful formula:
(Part / Whole) * 100 = Percentage
In this formula:
- Part: The number that represents a portion of the whole (in this case, 6).
- Whole: The total or reference number (in this case, 50).
- Percentage: The value we want to find, representing the part's proportion to the whole, expressed as a percentage.
This formula is the foundation for countless percentage-related calculations. It allows us to express any ratio as a percentage, making it easier to compare and understand different proportions. The concept of percentages originated from the need to standardize comparisons and make proportions more readily understandable in commerce and finance.
Percentages have a long and rich history, tracing back to ancient Rome. The Romans used a system of fractions based on 1/100, which was often used to calculate taxes on goods sold at auction. As trade and commerce evolved, the need for standardized financial calculations became increasingly important. During the Middle Ages, the concept of percentages gradually gained wider acceptance among merchants and mathematicians. The modern symbol for percent, "%", evolved over time from various abbreviations used to denote "per centum," Latin for "out of one hundred."
The formalization of percentage calculations provided a common language for expressing proportions, facilitating trade, financial transactions, and statistical analysis. Without percentages, it would be much more difficult to compare different quantities or to track changes over time. Today, percentages are integral to almost every aspect of our lives, from calculating discounts and interest rates to understanding statistics and survey results.
A Comprehensive Overview of Percentages
Let's delve deeper into the concept of percentages. A percentage is essentially a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." Therefore, when we say "x percent," we mean "x out of every 100."
The concept of percentages is closely related to fractions and decimals. Any percentage can be easily converted into a fraction or a decimal, and vice versa. This interconvertibility makes percentages a versatile tool for expressing and comparing proportions. For example:
- 25% is equivalent to the fraction 1/4 and the decimal 0.25.
- 50% is equivalent to the fraction 1/2 and the decimal 0.50.
- 75% is equivalent to the fraction 3/4 and the decimal 0.75.
Understanding these relationships is crucial for performing accurate calculations involving percentages. When dealing with complex calculations, it is often easier to convert percentages into decimals or fractions before performing the arithmetic operations.
Percentage calculations are used to express proportional changes. For example, if a price increases from $10 to $12, the percentage increase is calculated as:
((New Value - Old Value) / Old Value) * 100 = Percentage Increase
In this case:
(($12 - $10) / $10) * 100 = 20%
This means that the price increased by 20%. Similarly, percentage decreases can be calculated using the same formula, ensuring the absolute value of the new and old values are taken into account.
Percentages also play a crucial role in statistics. They are used to express probabilities, confidence intervals, and statistical significance. In survey research, percentages are used to summarize and present data in a clear and understandable format. For example, a survey might report that 60% of respondents agree with a particular statement. This allows for easy interpretation of the results and comparison across different groups or studies.
Trends and Latest Developments in Percentage Usage
In today's data-driven world, the application of percentages has expanded significantly. From finance to healthcare, percentages are used to analyze trends, make predictions, and inform decision-making. Let's explore some of the latest developments and trends in percentage usage:
- Financial Analysis: In finance, percentages are used to calculate returns on investment, interest rates, and risk assessments. The use of percentage-based metrics allows investors to compare the performance of different investments, regardless of their absolute size. Modern financial models rely heavily on percentage calculations to forecast future performance and manage risk.
- E-commerce and Marketing: E-commerce platforms use percentages extensively to track conversion rates, click-through rates, and customer engagement. Marketers use these metrics to optimize their campaigns and improve the return on investment. A/B testing often involves comparing the percentage change in key performance indicators (KPIs) to determine which version of a marketing message or website design is most effective.
- Healthcare: In healthcare, percentages are used to track infection rates, mortality rates, and treatment success rates. These metrics help healthcare professionals monitor the quality of care and identify areas for improvement. Public health officials use percentage data to track the spread of diseases and evaluate the effectiveness of interventions.
- Data Science and Analytics: Data scientists use percentages to summarize and visualize data, making it easier to identify patterns and trends. Percentage changes are often used to highlight significant differences between groups or time periods. Machine learning algorithms use percentage-based metrics to evaluate the performance of predictive models.
According to recent surveys, many professionals feel that a strong understanding of percentages is crucial for their career advancement. A survey by the National Numeracy Network found that employees who are comfortable working with percentages are more likely to be promoted and earn higher salaries. This underscores the importance of developing strong numeracy skills, including the ability to perform percentage calculations quickly and accurately.
Expert opinions emphasize the importance of using percentages responsibly and ethically. It is crucial to provide context and avoid misleading interpretations of percentage data. For example, a large percentage increase might seem impressive, but it could be insignificant if the base number is very small. Similarly, a small percentage decrease might be meaningful if the base number is very large.
Tips and Expert Advice for Working with Percentages
Now that we have a comprehensive understanding of percentages, let's explore some practical tips and expert advice for working with them effectively:
-
Always Define the Base: When working with percentages, it is crucial to clearly define the base or the whole. The percentage is meaningless without a clear understanding of what it is being applied to. For example, if a store offers a 20% discount, it is important to know whether the discount is being applied to the original price or some other value.
-
Convert Percentages to Decimals: When performing calculations involving percentages, it is often easier to convert them to decimals. To convert a percentage to a decimal, simply divide by 100. For example, 25% becomes 0.25. This makes it easier to perform arithmetic operations and avoid errors.
-
Use Percentages to Compare Proportions: Percentages are a powerful tool for comparing proportions. When comparing two different quantities, expressing them as percentages allows for a direct comparison, regardless of their absolute size. For example, if one investment yields a 10% return and another yields a 15% return, it is easy to see that the second investment is more profitable, even if the initial investment amounts are different.
-
Be Mindful of Percentage Change: When calculating percentage changes, it is important to use the correct formula and avoid common pitfalls. The percentage change is calculated as:
((New Value - Old Value) / Old Value) * 100
It is important to use the original value as the base and to pay attention to the sign (positive or negative) of the change.
-
Understand Compound Interest: Compound interest is a powerful concept that involves earning interest on both the principal and the accumulated interest. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A is the future value of the investment/loan, including interest
- P is the principal investment amount (the initial deposit or loan amount)
- r is the annual interest rate (as a decimal)
- n is the number of times that interest is compounded per year
- t is the number of years the money is invested or borrowed for
Understanding compound interest is crucial for making informed financial decisions.
FAQ About Percentages
Q: What is the difference between percentage and percentile?
A: A percentage expresses a part of a whole as a fraction of 100, while a percentile indicates the value below which a given percentage of observations in a group of observations falls.
Q: How do you calculate percentage increase?
A: Percentage increase is calculated using the formula: ((New Value - Old Value) / Old Value) * 100.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100% if the new value is more than double the old value. For example, if a company's revenue doubles, the percentage increase is 100%.
Q: What is a percentage point?
A: A percentage point is the arithmetic difference between two percentages. For example, if a rate increases from 10% to 12%, that's an increase of 2 percentage points.
Q: How are percentages used in statistics?
A: In statistics, percentages are used to summarize data, express probabilities, and calculate confidence intervals. They provide a standardized way to compare different groups or studies.
Conclusion
So, what percent of 50 is 6? Applying the formula (Part / Whole) * 100, we get (6 / 50) * 100 = 12%. Therefore, 6 is 12% of 50. Understanding and calculating percentages is an invaluable skill applicable across numerous aspects of life, from everyday shopping to complex financial analyses. By mastering this skill, you empower yourself with a powerful tool for interpreting data, making informed decisions, and navigating the world around you with confidence.
Now, put your newfound knowledge to the test! Think about your daily expenses. What percentage of your monthly income goes towards rent or groceries? Analyzing your spending habits through the lens of percentages can offer valuable insights into your financial health. Take a moment to calculate these percentages and share your findings – let's start a conversation about practical applications of percentage calculations in our lives!
Latest Posts
Latest Posts
-
3 4 Lb Is How Many Oz
Nov 26, 2025
-
What Is A Simple Predicate In Grammar
Nov 26, 2025
-
What Percent Of 50 Is 6
Nov 26, 2025
-
Valley Of Ashes In The Great Gatsby
Nov 26, 2025
-
What Is The Difference Between A Closed And Open System
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 50 Is 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.